算法笔记-杂乱版持续更新

算法模板：数学、二分、双指针、单调栈、单调队列、字典树、Z函数、dp、差分、堆、线段树

蓝桥杯省赛考点

统计结果如下：

知识点 出现次数
模拟 17
贪心 16
DP 14
枚举 11
数学 9
二分 8
数论 7
DFS 5
前缀和 5
推公式 5
快速幂 4
差分 4
双指针 4
状态压缩DP 4
思维题 4
BFS 3
树形DP 3
递推 3
字符串处理 3
排序 2
搜索 2
剪枝 2
递归 2
动态规划 2
分类讨论 2
线性DP 2
最大公约数 2
二叉树 2
背包问题 2
找规律 2
并查集 2
哈希表 2
分解质因数 2
堆 2
结论题 1
树的直径 1
斐波那契数列性质 1
龟速乘 1
树状数组 1
归并排序 1
矩阵乘法 1
哈希 1
区间DP 1
辗转相减法 1
图论 1
环 1
置换群 1
完全背包问题 1
扫描线 1
线段树 1
Flood Fill 1
均值不等式 1
滑动窗口 1
平衡树 1
STL Set 1
IDA* 1
日期问题 1
贡献法 1
Bellman-Ford 1
SPFA 1
Dijkstra 1
组合计数 1
栈 1
括号序列 1
博弈论 1
构造 1
图的遍历 1
概率论 1
数学期望 1
逆元 1
快速选择 1
链表 1
排序不等式 1
多路归并 1
整数分块 1
整除 1
单调队列 1
欧拉函数 1
状态机 1
区间合并 1

蓝桥杯官方刷题

0走方格 - 蓝桥云课 (lanqiao.cn)

python刷算法技巧/知识

python 蓝桥杯之常用的库_蓝桥杯python库-CSDN博客

【蓝桥杯】Python自带编辑器IDLE的使用教程_python蓝桥杯编译器-CSDN博客

蓝桥杯 python组IDLE的使用方法_蓝桥杯能打开idle自带的文档吗-CSDN博客

F1打开帮助文档！！！

1. map事实上是返回一个迭代器

2. 注意如果在函数里面需要使用一个全局变量

   • global ans

   • nonlocal ans

   • 先像上面这两种方法声明一下

3. 区分 t[::-1]和 t[:-1]

   • 前者：用于反转序列，返回序列的反向版本
   • 后者： 用于获取序列的子序列，该子序列包含从序列的第一个元素到倒数第二个元素（不包括最后一个元素），没有反转

4. 格式化输出

   # 格式化输出十进制
   decimal_format = "The number in decimal is: %d" % number
   print(decimal_format)  # 输出: The number in decimal is: 255

5. python正无穷：inf，需要先从math引入

   from math import inf

6. isqrt(mid//i) 比 int(sqrt(mid//i)) 快很多吗，大概五倍，也要从math库引入

   from math import inf

7. join的使用

   print(' '.join(i for i in map(str,path)))

8. python里面自己来调用 min，max很慢，如果觉得很慢可以自己拆开了用if，else来写。那么怎么定义”很慢“呢？

9. 输入

   #读取n个数 
   a = list(map(int, input().split()))

10. 输入数据太多比如10^5以上建议用 sys.stdin

    import sys 
    input = lambda : sys.stdin.readline().strip()

11. s.sort() 和 sorted(s) 的区别：（一般习惯用s.sort()）

    注意s.sort() 直接在s里面修改，不会返回一个新的

    但是 sorted(s) 不会在s里面修改，而是返回一个新的

12. 创建多维数组：

    比如 n*m 的数组，注意先 m 后 n

    a = [[ 0 for _ in range(m)] for _ in range(n)]

    创建一个a * b *c 的数组，初始化为全0

    f = [[[0 for _ in range(c)] for _ in range(b)] for _ in range()]

13. min(列表1的一部分，列表1的另一部分)是不可以的

    在Python中，min 函数不能直接接受两个列表作为参数，然后比较这两部分来决定最小值。min 函数期望的是一个可迭代对象，从中它会找到最小值。如果你尝试将两个列表作为参数传递给 min，你将得到一个类型错误，因为 min 函数不知道如何比较两个列表。

14. 手动实现上取整：

(x+mid-1)//mid #这一步，实现上取整，怎么实现的？ 
                # 上取整，其实可以测试一下 (x-1) // mid
                # 如果 x是mid的倍数，那么这个结果就应该加1（恢复原样）
                # 如果 x不是mid的倍数，那么这个结果也应该加一（上取整）

15. python自带的bisect使用：

    bisect_left：（最左）如果要查找 最左边的，使用bisect_left 找如果要插入，应该插入的最左端位置，如果列表中已经存在该元素，它将返回该元素在列表中的最左侧位置

    bisect_right：（最右）返回的是插入点的右侧位置，即如果列表中已经存在该元素，它将返回该元素在列表中的最右侧位置

    bisect：bisect是bisect_right的别名，所以它的使用方式与bisect_right完全相同

    from bisect import *
    
    # 有序列表
    a = [1, 3, 5, 7, 9]
    
    # 要插入的元素
    x = 5
    
    # 使用bisect_left找到插入点
    index = bisect.bisect_left(a, x)
    
    print("插入点的索引:", index)
    # 输出: 插入点的索引: 2
    
    index = bisect.bisect_right(a, x)
    print("插入点的索引:", index)  # 输出: 插入点的索引: 3

16. 其实列表就是栈，Python中列表的实现是基于链表来的，python中的列表里的pop（）可以实现出栈，append（）实现入栈，而这两个操作的时间复杂度都是o（1），所以列表本身就是一个栈，实现队列的话用pop（0）实现出队，append（）实现入队，只不过这里的pop（0）的时间复杂度是o（n）

    所以队列最好还是用deque的popleft和append，这两个时间复杂度是o（1）

    使用队列：

    import collections
    q = collections.deque()
    
    #左端出队
    q.pop_left()
    #右端入队
    q.append()
    
    #判断队列是否为空
    len(q) > 0

17. 熟悉一下文件操作，可能需要你打开文件？

    逆元，博弈

18. 排序：按照某个key排序

    • 按照元组的第二个元素排序：

      arr = [(1, 3), (4, 1), (2, 2), (5, 0)]
      arr.sort(key=lambda x: x[1])

    • 按照字典的某个键排序：

      # 使用 sort 方法按字典的 'age' 键排序
      arr.sort(key=lambda x: x['age'])

19. 千万不要像这样初始化数组：

    nums = [[0,0]]*n

    使用列表推导式而不是乘法的原因是，乘法会创建对同一个列表对象的多个引用，这可能会导致意外的副作用。例如：

    python复制代码# 错误的方法：使用乘法
    n = 5
    my_list = [[0, 0]] * n
    
    # 修改一个元素会影响所有元素，因为它们引用的是同一个对象
    my_list[0][0] = 1
    print(my_list)  # 输出 [[1, 0], [1, 0], [1, 0], [1, 0], [1, 0]]

    在上面的例子中，[[0, 0]] * n 会创建一个包含对同一个 [0, 0] 列表的 n 个引用的列表。因此，修改其中一个元素会导致所有元素都发生变化。

    因此，推荐使用列表推导式来避免这种问题：

    python复制代码n = 5
    my_list = [[0, 0] for _ in range(n)]
    
    # 修改一个元素不会影响其他元素
    my_list[0][0] = 1
    print(my_list)  # 输出 [[1, 0], [0, 0], [0, 0], [0, 0], [0, 0]]

    这样可以确保每个元素都是独立的 [0, 0] 列表，不会相互影响。

20. python对部分数组排序

    tmp[i:j+1] = sorted(tmp[i:j+1])
    # tmp[i:j+1].sort()是错误的，不会作用于原数组
    # 创建的是原数组的一个切片（即一个新的列表），并对这个新的列表进行排序，而不会影响原数组

21. ascii转字符串：chr()

    字符串转ascii：ord()

22. 四舍五入: round(n)

由数据范围反推算法复杂度以及算法内容

1.数学

1.2试除法判定质数

质数： > 1且约数只包含1 和本身

性质： d | n， (n/d) | n

因此n的所有约数其实都是成对出现的，因此我们可以每次只枚举每一对里面较小的那一个，也就是满足 d <= n/d，整理一下就得到 d <= 根号n，因此我们只需要枚举到根号n就可以，从而降低了时间复杂度

n中最多只包含一个大于sqrt(n)的质因子，如果有两个，相乘不就 > n了吗

快速求因数

只用从 $1$ 到 $\sqrt{n}$ 枚举因数，另一个因数就等于 $n \div 当前因数$ ，必被整除的

for x in nums1:
    for i in range(1,isqrt(x)+1):
        if x%i == 0:
            dict[i] += 1
            if i*i < x: # 等于x的话就重复计算了
                dict[x//i]+=1

快速排序

1. 确定分界点，q[(l+r)//2] or q[random]
2. 调整区间： 让所有 <=x 的在x左边，>= x的在x右边
3. 递归处理左右区间

最难实现的就是第二步了：

• 容易想到但是不优美的做法：

  可以开两个额外的数组，把 <= x的放在一个，>=x 的放在另一个，最后把他们俩拼起来

• 优雅做法：

  • 用两个指针，其中 i 指向第一个，j 指向最后一个
  • 遇到 <=x 的数，i++，直到遇到第一个 >x 的数，停下
  • 遇到 >=x 的数，j–，直到遇到第一个 <x 的数，停下
  • 交换 i 和 j 对应的数
  • 循环直到 i > j

1.3离散化

数的值域很大，但是范围不大（稀疏），需要用到数的值做下标，但是又不可能开那么大的全局数组，于是需要离散化：把数值映射

需要解决的问题：

• 去重（先排序后unique去重）
• 如何算出 x 离散化之后的值（二分）

一般来说 10的五次方以内差不多

把下标在 i 的值，映射到一个数

1.4模运算

分享丨模运算的世界：当加减乘除遇上取模 - 力扣（LeetCode）

加法和乘法的取模：
$$
(a+b)\ mod\ m=((a\ mod\ m)+(b\ mod\ m))\ mod\ m
$$

$$
(a b)\ mod\ m=((a\ mod\ m)(b\ mod\ m))\ mod\ m
$$

负数的取模： $x<0$ ，$y>=0$，则 $x \equiv y\ mod\ m$ 等价于
$$
x\ mod\ m+m=y\ mod\ m
$$

除法的取模：如果 𝑝 是一个质数，𝑎是 𝑏的倍数且 𝑏和 𝑝互质（𝑏不是 𝑝的倍数），那么有
$$
\frac{a}{b}\ mod\ p =(a*b^{p-2})\ mod\ p
$$

总结
代码实现时，上面的加减乘除通常是这样写的：

MOD = 1_000_000_007

// 加
(a + b) % MOD

// 减
(a - b + MOD) % MOD

// 乘
a * b % MOD

// 多个数相乘，要步步取模，防止溢出
a * b % MOD * c % MOD

// 除（MOD 是质数且 b 不是 MOD 的倍数）
a * qpow(b, MOD - 2, MOD) % MOD

1.5 gcd 与 lcm

def gcd(a,b):
  if a<b:
    a,b=b,a
  while b!=0:
    a,b=b,a%b
  return a

def lcm(a,b):
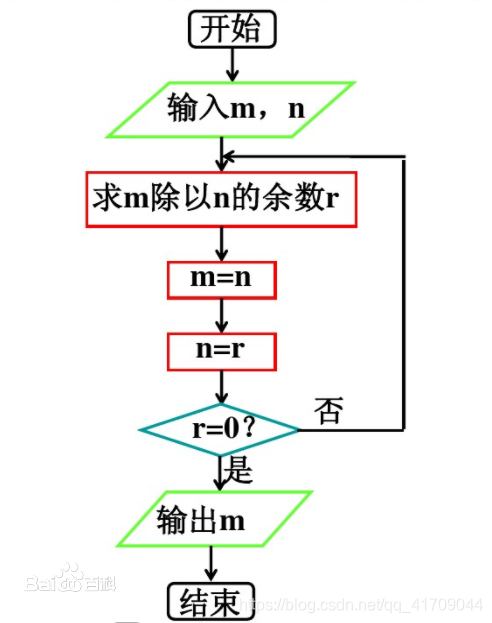
	return (a*b)/gcd(a,b);

gcd(a,b) = gcd(b,a)

2.双指针 变长滑动窗口

两数之和，三数之和：

• 什么时候可以使用双指针？
  • 双指针要求一定要排序，排序之后元素对应的下标就变了
  • 因此如果题目要求返回元素数值我们就可以使用双指针
• 使用hash表
  • 题目要求返回下标时

双指针要满足单调性

在什么时候移动指针

什么时候记录答案要搞清楚

209. 长度最小的子数组 - 力扣（LeetCode）

713. 乘积小于 K 的子数组 - 力扣（LeetCode）

[3. 无重复字符的最长子串 - 力扣（LeetCode）](

3.二分

红蓝染色法理解二分

我们以寻找到 >= x 的第一个下标来举例：

你的条件可以灵活定义

用红色表示不满足条件的，蓝色表示满足条件的，白色表示不确定

核心：

• 你要维护的区间内的都是没有染色的，区间的定义是未染色的范围，而不是答案的范围！！！
• l 和 r 的初始值怎么定义？看你初始的不知道如何染色的区间范围（白色）是多少，以及你二分是使用闭区间 or 开区间 or 左闭右开 哪种策略编写的，据此定下来你的 l 和 r值
• 循环条件如何终止？当你的区间不为空的时候循环
• 中间判断了之后 l，r 与 m 的关系应该怎么变化：看你想要寻找什么
• 最后答案应该怎么return：在找第一个 >= x 的情况下你要return的应该是蓝色（true）的第一个

mid 表示正在询问的数

闭区间写法下我们如何取得答案？

有一个循环不变量保持着：

• L-1始终是红色
• R+1始终是蓝色
• 那么答案其实就是 蓝色的第一个，也就是L或者R+1

多种写法

一般求什么就二分什么

三种写法：推荐开区间，中间l,r,m之间的判断关系简单

# 找 >= target 的第一个
def lower_bound(nums,target):
    l = -1
    r = len(nums)
    #开区间写法
    # mid 满足要求时，更新的是谁就返回谁
    while l+1 < r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m   #(m,r)
        else:
            r = m #(l,m)
    return r

def lower_bound2(nums,target):
    #闭区间写法
    l = 0
    r = len(nums)-1
    while l<=r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m+1   
        else:
            r = m-1 
    return l

def lower_bound3(nums,target):
    l = 0
    r = len(nums)
    #左闭右开区间写法 
    while l < r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m+1   
        else:
            r = m 
    return r

那么一共演变了四种题型：

>= x 	这种是我们熟知的
> x 	这种可以转化为 >= x+1
< x 	这种可以转为 >=x 的下标 -1
<= x	这种可以转为 >x 的下标 -1 即 >= x+1

如果说target比所有的数都大的话：会返回数组最大下标的next

target比所有的数都小的话：会返回 0

target在最大最小范围内，但是没有target，会返回 >= target 的第一个

python 写二分最好还是直接调用库，这样比较快，大概快一半

from bisect import *
bisect_left(nums,target) #返回 >= target的第一个，行为与我自己写的完全一致

162

https://leetcode.cn/problems/find-peak-element/

#红色代表峰顶左边
#蓝色代表峰顶以及峰顶右边
#区间表示不知道染什么色的东西
#只需要比较mid和mid+1就行，找到第一个下坡？
#如果你往下坡方向走，也许可能遇到新的山峰，但是也许是一个一直下降的坡，最后到边界。
#但是如果你往上坡方向走，就算最后一直上的边界，由于最边界是负无穷，所以就一定能找到山峰
#总的一句话，往递增的方向上，二分，一定能找到，往递减的方向只是可能找到，也许没有
def lower_bound(nums):
    l = -1 #[0,n-2]
    r = len(nums) - 1
    while l+1<r:
        mid = (l+r) // 2
        if nums[mid] < nums[mid+1]:
            l = mid #染红色
        else:
            r = mid #染蓝色
    return r
class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        return lower_bound(nums)

153

原题链接： 153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

分析

这题一共就两种情况，因为是对一个有序数组的旋转，看下面画的图

第一种情况很好解决，简单的二分，第二种情况需要分析一下

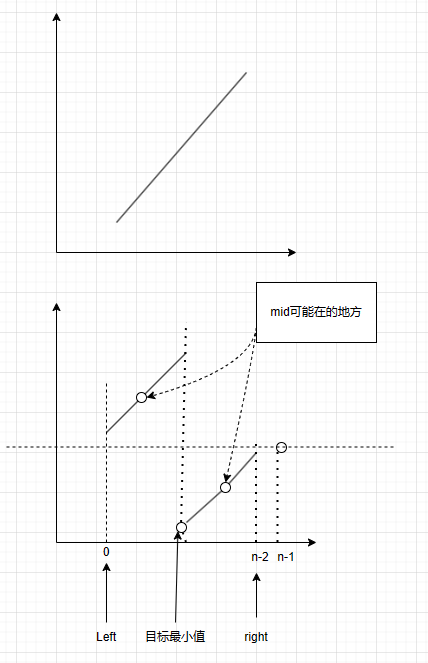
我们要找的相当于是谷底，也就是左右都比他大的

红蓝染色法二分：

• 红色表示最小数的左边
• 蓝色表示最小数或者最小数的右边

我们可以首先确定最后一个数一定是蓝色，所以开始的区间可以设为 [0,n-2]，这个区间是我们不知道要怎么染色的，接下来开始二分缩小这个区间

使用开区间来写的话，最初 l = -1，r = n-1

那么我们怎么确定要染什么颜色？

• 通过已知条件来看，我们仿照上一题，让mid和mid+1来比较可以吗？显然是不行的，因为除了最小值旁边的元素其他位置都满足 num[mid] < num[mid+1] ，无法根据这个来染色
• 可以根据 num[mid] 和 num[-1] (最后一个元素) 来比较
  • 如果 num[mid] < num[-1]：由图可知，需要让 r = mid
  • 如果 num[mid] > num[-1]：由图可知：需要让 l = mid

最后返回值应该是什么呢，下标返回 r 即可

code

# 这题不就是寻找谷值吗
# 红色表示谷左边
# 蓝色表示谷以及谷的右边
def binsearch(nums):
    l = -1 # [0,n-2]
    r = len(nums) - 1
    while l+1 < r:
        mid = (l+r) // 2
        if nums[mid] < nums[-1]:
            r = mid 
        else:
            l = mid
    return nums[r]
class Solution:
    def findMin(self, nums: List[int]) -> int:
        return binsearch(nums)

思考：

边界条件，最小的在最右怎么办?

• 这种情况由于一开始其实我们就给最右染色了，那么 r 一直是不会移动的，合理

一般最大化最小值或者最小化最大值都可以用二分来做

4.单调栈

单调栈：如果你发现你要计算的内容和上一个更大（小）/下一个更大/（小）的元素有关，尝试单调栈

栈中保存有用的，维护它的单调性【这一点是最难的，你如果知道需要保留什么，就知道什么东西需要入栈，什么东西需要出栈，在什么时候计算答案】

可以在进栈 or 出栈的时候来做你想做的

原题链接：739. 每日温度 - 力扣（LeetCode）

从左往右

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        st = [] # st 存的下标
        ans = [0]*len(temperatures)
        for i,x in enumerate(temperatures):
            while st and x > temperatures[st[-1]]:
                t = st.pop()
                ans[t] = i - t
            st.append(i)
        return ans

从右往左：

现在的是 x，弹出栈中所有 <= x的数（弹出意味着这些数没有用了，为什么呢，是因为x把右边的全部遮住了，我们左边的所有数的答案都不可能是和遮住的这些数有关）

那为什么比更大的数还要保留呢，如果一个数比x大并且小于这个栈顶更大的数，那么这个数的答案就是我们提到的更大的数

然后放入栈，x的答案是在发现栈为空（此时不用操作，初始化时已经设置为了0）或者栈顶元素比自己大了，此时可以算x对应的答案，然后放入x

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        st = [] # st 存的下标
        n = len(temperatures)
        ans = [0]*n # 这里的初始化很重要，对于没有下一个更高温度的，在下面是不会处理它的
        for i in range(n-1,-1,-1):
            x = temperatures[i]
            while st and x >= temperatures[st[-1]]: # 注意这里要 x>= 不然对于一样的会有错误比如 3,5,5,6,2
                t = st.pop()
            if st:
                ans[i] = st[-1] - i
            st.append(i)
        return ans

注意最后，栈不一定是空的

个人更偏向从左往右

对栈顶元素找上一个更大的元素，在找的过程中填坑

横着计算，看成水泥，填平了，那么 <= 自己的高度就不需要了，因为已经填平

需要的下标：当前元素的下标，栈顶元素的下标，栈顶元素的上一个的下标

这个栈里面存的是从右往左能看到的东西

每次必入栈，出栈不一定

class Solution:
    def trap(self, height: List[int]) -> int:
        ans = 0
        st = []
        for i,x in enumerate(height):
            #要找下一个更小和下一个>=自己的
            # 出栈的,清除掉 <= x的
            left = 0
            bottom = 0
            right = 0
            while st and  x >= height[st[-1]]: #这里 > 或者 >= 都可以，如果是>=的话 min(right,left)-bottom 就等于 0 ，其实 >= 更好，比如2,2,0,1，其
                if len(st) >= 2:
                    bot = st.pop()
                    l = st[-1] #注意这个不能出栈，这个还有用，只有栈顶没用了，被水泥封上了
                    bottom = height[bot]
                    left = height[l]
                    right = x
                    ans += (min(right,left)-bottom)*(i-l -1)
                else:
                    st.pop()
            st.append(i)
        return ans
                    

时间复杂度

0最大区间 - 蓝桥云课 (lanqiao.cn)

需要特别注意，在数组的开头和末尾各自加上一个0 如果开头不加上0，会出现越界访问；如果末尾不加上0，会出现这种数据没有结果 5,1 2 3 4 5。原理是让最后一个0来让前面的所有没有更新的出栈更新至少一次

5.单调队列

及时去掉无用数据，保证双端队列有序

滑动窗口最大值

deque里面存的是下标

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        q = deque()
        ans = []
        for i,x in enumerate(nums):
            # 出
            while q and x >= nums[q[-1]]:
                q.pop()

            # 入
            q.append(i)
            #最大下标 i-k+1
            #为什么只看q[0]呢，因为我们只后移了一位相当于，只有队首有可能out了
            if q[0] < i-k+1: 
                q.popleft()
            #记录答案
            if i>=k-1:
                ans.append(nums[q[0]])
        return ans

复杂度：每个下标最多入队出队各一次，所以复杂度是O(n)

当前数字 >= 队尾，弹出队尾

弹出队首不在窗口内的元素

1438. 绝对差不超过限制的最长连续子数组 - 力扣（LeetCode）

def dq(nums,limit):
    q_min = deque()
    q_max = deque()
    ret =left= 0
    for i,x in enumerate(nums):
        while q_min and x < nums[q_min[-1]]:
            q_min.pop()
        q_min.append(i)
        # if q_min[0] < i-k+1:
        #     q_min.popleft()
        
        while q_max and x > nums[q_max[-1]]:
            q_max.pop()
        q_max.append(i)
        # if q_max[0] < i-k+1:
        #     q_max.popleft()

        while q_min and q_max and  nums[q_max[0]]-nums[q_min[0]] > limit:
            if nums[q_min[0]] == nums[left]:
                q_min.popleft()
            if nums[q_max[0]] == nums[left]:
                q_max.popleft()
            left += 1

        ret = max(ret,i-left+1)

    return ret


class Solution:
    def longestSubarray(self, nums: List[int], limit: int) -> int:
        # 任意两个元素之间的绝对差必须小于或者等于 limit 转化为 最大最小之差 <= limit
        n = len(nums)
        if n == 1 :
            return 1
        res = 0
        return dq(nums,limit)

注意这是没有 k 限制的滑动窗口

然后 ret = max(ret,i-left+1) 这里不能写成 ret = max(ret,i-min(q_max[0],q_min[0])+1)，因为窗口最左端的索引有可能已经被顶掉了，看下面这个样例。 nums = [4,10,2,6,1] limit = 10

所以需要额外的信息来保存最左端的索引

1438. 绝对差不超过限制的最长连续子数组 - 力扣（LeetCode）

https://leetcode.cn/problems/longest-substring-without-repeating-characters/)

6.字典树

注意下面所说的字母和字符串的区别

1. 把字符串按照前缀分组，第一个字母相同的，分到一组，第二个字母相同的，分到另一组….
2. 用一颗树来实现
3. 把每个字母对应到一颗树上的某个节点，保证对于每个字符串s内部，s[i]一定是s[i+1]的父节点

字典树可以用来快速判断一个字符串是否是另一个字符串的前缀，但是没办法判断后缀

后缀可以转为前缀 ，从后往前建树和查找不就行了

可以用两个前缀树，但是可以转化，把这两个信息整合到一个pair

什么时候想到用字典树呢，分组，组里面还有更小的组，这种就可能需要树：本质就是用树来分组

class Trie:

    def __init__(self):
        self.children = {}
        self.is_end_of = False

    def insert(self, word: str) -> None:
        current = self
        for char in word:
            if char not in current.children:
                current.children[char] = Trie()
            current = current.children[char]
        current.is_end_of = True    

    def search(self, word: str) -> bool:
        current = self
        for char in word:
            if char not in current.children:
                return False
            current = current.children[char]
        return True if current.is_end_of else False


    def startsWith(self, prefix: str) -> bool:
        current = self
        for char in prefix:
            if char not in current.children:
                return False
            current = current.children[char]
        return True


# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

入门字典树：208. 实现 Trie (前缀树) - 力扣（LeetCode）

3093. 最长公共后缀查询 - 力扣（LeetCode）

最大异或和

421. 数组中两个数的最大异或值 - 力扣（LeetCode）

7.Z函数 扩展kmp

但实际上和kmp没什么关系

计算每个后缀能和字符串开头匹配多长

利用已经匹配的信息

z-box右侧的字符都是没有见过的

回溯

回溯三问！！！

1. 当前操作
2. 子问题？
3. 下一个子问题？

8.dp

如何手动记忆化搜索

核心是两点：

• dfs改成数组
• 递归改成循环

# 由于有两个背包，所以二维肯定不行
# 考虑用两个数组或者三维
n,a,b = map(int,input().split())
nums = [0]*n
nums = list(map(int,input().split()))
# f[a][b][n] 表示余量为a,b，前n个物品的最大值
f = [[[0 for _ in range(n+1)] for _ in range(b+1)] for _ in range(a+1)]


 def dfs(i,j,k):
   if k<0:
     return 0
   if i < 0 or j <0:
     return 0
   if f[i][j][k] != -1:
     return f[i][j][k]
   if i >= nums[k]:
     suma = max(dfs(i,j,k-1),dfs(i-nums[k],j,k-1)+nums[k])
   else:
     suma = dfs(i,j,k-1)
   if j >= nums[k]:
     sumb = max(dfs(i,j,k-1),dfs(i,j-nums[k],k-1)+nums[k])
   else:
     sumb = dfs(i,j,k-1)
   f[i][j][k] = max(suma,sumb)
   return f[i][j][k]

注意看，if f[i][j][k] != -1 return f[i][j][k] 这一行就是利用记忆化搜索了

然后注意更新数组的位置 f[i][j][k] = max(suma,sumb) 别忘记了

在每次return之前更新对应的dp数组，然后dp数组的初始值可以给一个不可能达到的值，后面判断是不是这个值就可以知道是否搜索过了，从而实现记忆化搜索

注意你的结果是return dfs的结果而不是dp数组

dfs.cache_clear() # 防止爆内存

记忆化搜索：

3154. 到达第 K 级台阶的方案数 - 力扣（LeetCode）

注意如果很难确定数组大小，用hash表

注意遇到需要记录的dp数组，右边应该是dfs结果而不是dp数组结果

#正确
if s[i] == s[j]:
    f[i][j] = dfs(i+1,j-1)+2
    return f[i][j]
#错误
if s[i] == s[j]:
    f[i][j] = f[i+1][j-1]+2
    return f[i][j]
#然后要注意return的是 f[i][j] 而不是 dfs(i,j)不然又算了一遍哈，浪费时间

记忆化搜索翻译为递推时，要注意循环的顺序，看你是从什么转移过来的

• 从i+1这种更大的转移过来，那么就需要反序枚举
• 从i-1这种更小的转移过来，那么就需要正序枚举

还要注意是否增加下标防止数组越界，也就是看有没有-1的出现和n的出现（数组最大下标为n-）

背包

• 恰好：dfs时必须等于0才记录答案
• 至多：dfs时>=0记录答案，然后初始化要变一下
• 至少：这个没看懂

看评论七水佬的总结

递推的初始值就是递归的边界

判断一维数组时是否需要反序遍历，自己根据状态转移方程列一个表来比较看一下

在只用一个一维数组的情况下，要注意转移来源 1. 不能被覆盖 2. 必须已经计算出来。按照这个要求，正序遍历会导致 0-1 背包状态被覆盖，而完全背包则是正确的（转移来源被计算出来，且不存在被覆盖的问题）；逆序遍历对于 0-1 背包是正确的（转移来源是上一行的，早就被计算出来了且没有被覆盖），而完全背包则不行（转移来源没有被计算出来）。

像这样画个图就很好理解

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        # 假设添加+号的正数的和为p
        # s为 sum(nums)
        # 那么添加-号的负数绝对值之和就为 s-p
        # 那么题意就转化为 p-(s-p) = t
        # p = (s+t)/2，p是非负数，整数
        # 那这样本题就变成了从nums中选择一些数，他们的和恰好为 (s+t)/2，这个固定的数
        # 也就是背包问题
        target += sum(nums)
        n = len(nums)
        if target<0 or target%2:
            return 0
        target//=2
        # def dfs(i,c):
        #     if i < 0:
        #         return 1 if c == 0 else 0
        #     if c < nums[i]:
        #         return dfs(i-1,c)
        #     return dfs(i-1,c) + dfs(i-1,c-nums[i])
        # return dfs(n-1,target)

        #优化空间，每次只用到了i-1和i，那么第一个下标就只用2就好了，每次%2
        # f = [[0]*(target+1) for _ in range(2)]
        # f[0][0] = 1
        # for i in range(1,n+1):
        #     for c in range(target+1):
        #         if c < nums[i-1]:
        #             f[i%2][c] = f[(i-1)%2][c]
        #         else:
        #             f[i%2][c] = f[(i-1)%2][c] + f[(i-1)%2][c-nums[i-1]]
        # return f[n%2][target]

        # 优化空间之一维
                #优化空间，每次只用到了i-1和i，那么第一个下标就只用2就好了，每次%2
        f = [0]*(target+1)
        f[0] = 1
        for i in range(1,n+1):
            for c in range(target,-1,-1): #或者枚举范围 range(target,nums[i-1]-1,-1)，这样就不需要if了
                if c >= nums[i-1]:
                    f[c] = f[c] + f[c-nums[i-1]]
        return f[target]

类似背包问题循环顺序的思考：

假设你现在在c，要转移到(i+1,c)你转移的其中一个肯定是(i,c)

那么对于另一个，如果你是从图中这两个蓝色框转移过来，那么需要倒序遍历

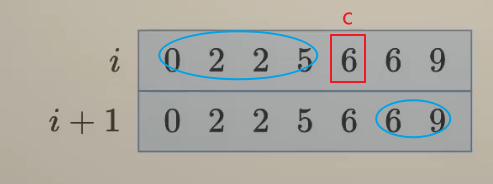
• 左上蓝色圈分析：你需要从一个左边的旧值转移过来，你如果正序遍历，那么左边的旧值会被新值覆盖，导致错误
• 右下蓝色圈分析：你需要从一个右边的新值转移过来，如果正序遍历，你得到的右边的还没有更新，还是旧值

如果是从这两个绿色框转移过来，那么需要正序遍历：

• 左下绿色圈分析：你需要从一个左边的新值转移过来，那么就要从左到右依次更新，如果你倒序遍历，左边的还是旧值没有更新
• 右上绿色圈分析：你需要一个右边的旧值转移过来，那么不能从右边更新过来，如果倒序遍历，右边的旧值会被新值覆盖，导致错误

如果察觉到重复的子问题，就可以使用动态规划（记忆化搜索）

从第一个或者最后一个开始思考?

如何满足恰好？ 在dfs返回值的时候判断此时背包剩余容量是不是0

线性dp

• 1143. 最长公共子序列
• 583. 两个字符串的删除操作
• 712. 两个字符串的最小 ASCII 删除和
• 72. 编辑距离

• 300. 最长递增子序列

前缀或者后缀

区间dp

不再是前缀或者后缀，而是数组中间的区间

核心思想是分治法？

1039. 多边形三角剖分的最低得分 - 力扣（LeetCode）

375. 猜数字大小 II - 力扣（LeetCode）

状态压缩dp

一般看到很小的数据范围，就有可能是一个状压dp，什么十几啊这种

9.差分数组

分享｜【算法小课堂】差分数组（Python/Java/C++/Go/JS） - 力扣（LeetCode）

优化对区间每个数都加/减同一个数的操作

记录变化量来优化

也可以这样理解，d[i] 表示把下标 >= i 的数都加上 d[i]。

性质 1：从左到右累加 𝑑 中的元素，可以得到数组 𝑎

代码模板

# 你有一个长为 n 的数组 a，一开始所有元素均为 0。
# 给定一些区间操作，其中 queries[i] = [left, right, x]，
# 你需要把子数组 a[left], a[left+1], ... a[right] 都加上 x。
# 返回所有操作执行完后的数组 a。
def solve(n: int, queries: List[List[int]]) -> List[int]:
    diff = [0] * n  # 差分数组
    for left, right, x in queries:
        diff[left] += x
        #
        if right + 1 < n:
            diff[right + 1] -= x
    for i in range(1, n):
        diff[i] += diff[i - 1]  # 直接在差分数组上复原数组 a
    return diff

这题目前还看不懂：2528. 最大化城市的最小电量 - 力扣（LeetCode）

10.堆，优先队列

1046. 最后一块石头的重量 - 力扣（LeetCode）

手写小顶堆：1046. 最后一块石头的重量 - 力扣（LeetCode）

python库实现的是小顶堆：heapq 是 Python 中的一个内置模块（不需要导入？）

import heapq
a = []
heapq.heapify(a) #将一个可迭代对象转换为堆数据结构
heapq.heappush(a,1) #向堆中添加一个新元素
heapq.heappop(a) #从堆中弹出并返回最小元素
heapreplace(heap, item) #弹出并返回最小元素，并将新元素推入堆中
nlargest(n, iterable) #返回可迭代对象中的前 n 个最大元素
nsmallest(n, iterable) #返回可迭代对象中的前 n 个最小元素

堆顶就是第0个元素

如果你需要实现大顶堆（最大优先队列），可以通过将优先级的值取负来实现：

0选段排序 - 蓝桥云课 (lanqiao.cn)

11.树状数组，线段树

https://www.bilibili.com/video/BV1ce411u7qP

动机，我们想修改一个点，然后查询某个区间的和

可选的方法：

• 维护 $n^2$ 个区间的和：此时查询是 $O(1)$，但是更新某个点是$O(n^2)$
• 把每个区间分成单个，也就是[1,1], [2,2] .. [n,n]，这样的话更新某个点是$O(1)$，查询是$O(n)$

这里查询和更新就像天平的两端，你需要做一个tradeoff

那么我们试着把维护的区间多一点，但是又不至于到 $n^2$ 个

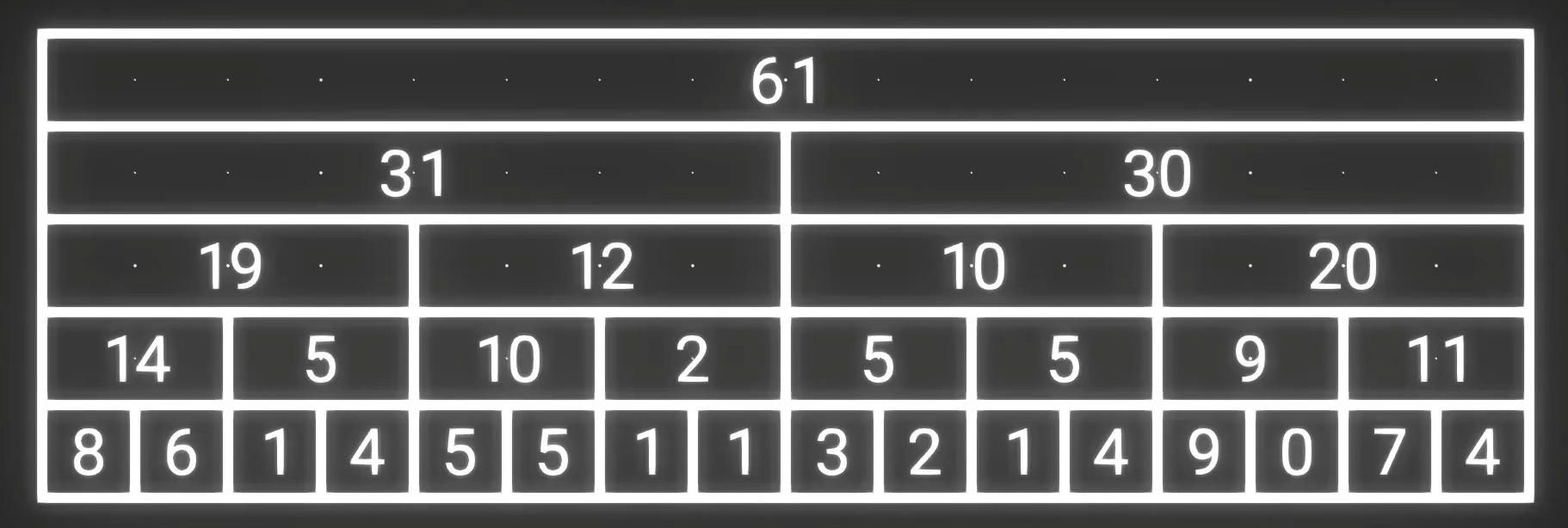
像这张图一样：此时我们要查询某个区间的和，复杂度其实降到了$O(logn)$

上面看上去就像树形结构了，好了，此时你就发明了线段树了()

代码实现：

首先我们需要开多大的数组，图上面这个数组最下面一层16，然后8,4,2,1

$16+8+4+2+1=31$

你的数组长度要差不多 $2^{n的二进制长度}*2$ 或者 4n

把最下面一层补满

树状数组：单点更新，区间查询
线段树：区间更新（都加上一个数、把子数组内的元素取反），区间查询

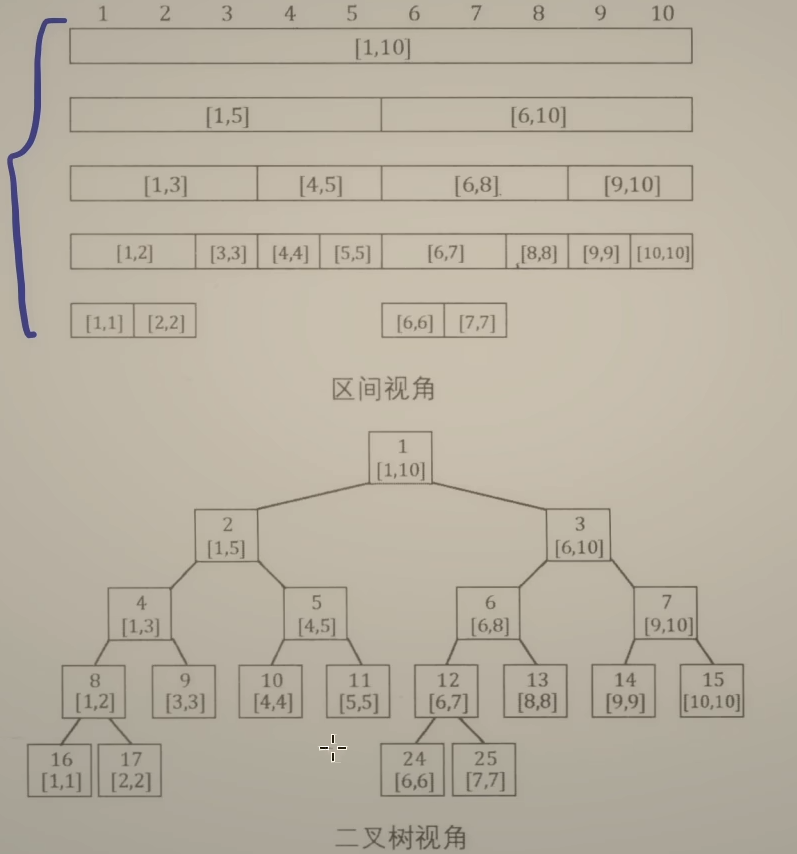
两大思想：

1. 挑选O(n)个特殊区间，使得任意一个区间可以拆分为O(logn)个特殊区间

   特殊区间个数 <= 4n

   最坏情况下，左边走到叶子结点，右边走到叶子结点，一共就拆分了2*树高 = 2 *logn个区间，也可以最近公共祖先来思考

o 表示结点编号

特别注意：由于o和0离得比较近切像，不要打错了！！！

def build(o:int, l:int, r:int):#相当于自底向上建树
    if l==r:
        #更新...
        d[o] = a[l]
        return
    m = l+r>>1
    #递归对左右区间建树
    build(o*2,l,m)
    build(o*2+1,m+1,r)
    #维护...
    d[o] = d[o*2] + d[o*2+1]

#区间查询
def getsum(o:int, l:int, r:int, L:int, R:int)->int:
    # [L,R]表示固定的你需要查询的区间
    # [l,r]表示当前节点包含区间
    if L<=l and r<=R: 
        return d[o] #当前区间为询问区间的子集时直接返回当前区间的和
    m = l+r>>1
    sum = 0
    # 如果左儿子代表的区间 [l, m] 与询问区间有交集, 则递归查询左儿子
    if L<=m:sum+=getsum(o,l,m,L,R)
    # 如果右儿子代表的区间 [m+1, r] 与询问区间有交集, 则递归查询左儿子
    if m+1<=R:sum+=getsum(o,m+1,r,L,R)
    return sum
    
    
    #[L,R]表示固定的，你需要update的区间
def update(o:int, l:int, r:int, L:int, R:int):
    if L<=l and r<=R: 
        #更新...
        return
    m = l+r>>1
    if m>=L:update(o*2,l,m,L,R)
    if m+1<=R:update(o*2+1,m+1,r,L,R)
    #维护...

单点修改不用lazy？区间修改才用lazy

单点修改直接到底了 不需要lazy延迟?

lazy更新

如果说我要更新的区间被完全包含在了这次更新的区间内，那就不继续往下走，而是添加一个lazy tag

如果这个区间在后续的更新、查询被破坏掉了，就把lazy tag往下传

lazy标记下，区间修改和查询操作的实现

todo = [0]*4*n #todo数组表示lazy标记
#注意lazy tag打在的这个区间是已经更新了的，只是他的自区间还没有更新

# 区间修改
# c表示被修改区间的变化量
def update(o:int, l:int, r:int, L:int, R:int, c:int):
    if L<=l and r<=R: # 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
        d[o] += (r-l+1)*c
        todo[o] += c
        return 
    m=l+r>>1
    if todo[o] and l!=r: #如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
        #如果l==r代表到了叶结点，下面没有子节点了，不用更新子节点
        #更新当前节点两个子结点的值
        d[o*2] += todo[o]*(m-l+1)
        d[o*2+1] += todo[o]*(r-m)
        # 将标记下传给子节点
        todo[o*2] += todo[o]
        todo[o*2+1] += todo[o]
        #清空当前节点的标记
        todo[o] = 0
        
    if m>=L:update(o*2,l,m,L,R,c)
    if m+1<=R:update(o*2+1,m+1,r,L,R,c)
    d[o] = d[o*2]+d[o*2+1]
    
#区间查询
def getsum(o:int, l:int, r:int, L:int, R:int)->int:
    if L<=l and r<=R:
        return d[o]
    m = l+r>>1
    if todo[o]:
        d[o*2] += todo[o]*(m-l+1)
        d[o*2+1] += todo[o]*(r-m)
        todo[o*2] += todo[o]
        todo[o*2+1] += todo[o]
        todo[o] = 0
    sum = 0
    if m>=L: sum+=getsum(o*2,l,m,L,R)
    if m+1<=R:sum+=getsum(o*2+1,m+1,r,L,R)
    return sum

如果要实现区间修改为某个值而不是加上某一个值的话：把+=改为=

注意，下面这个是oi-wiki的模板，不是我的，等待修改为我的版本

def update(o:int, l:int, r:int, L:int, R:int, c:int):
    if L<=l and r<=R:
        d[o]

资源

灵神主页题单：灵茶山艾府 - 力扣（LeetCode） 在讨论发布里面

分享｜从集合论到位运算，常见位运算技巧分类总结！ - 力扣（LeetCode）

n,p,q = map(int,input().split())

f = [0] + list(map(int,input().split()))

# 求f[q]-f[p]的最大值，选一段来排序
# 先向着左边扩展 [p,q]扩展为[0,q]
# 双堆模拟，大根堆，小根堆
# 其实不用小根堆
mint = inf
maxt = 0

h2 = [] #大根堆，存的相反数
for i in range(p,q+1):
  maxt = max(maxt,f[i])
  mint = min(mint,f[i])
  heapq.heappush(h2,-f[i])
res = maxt-mint
#开始向右扩展
for i in range(q+1,n+1):
  # 找此时的最小值，也就是f[p]
  mint = min(mint,f[i])
  # 找此时的最大值，也就是f[q]
  # 取出大根堆top
  heapq.heappush(h2,-f[i])
  heapq.heappop(h2)
  maxt = -h2[0]
  res = max(res,maxt-mint)

h2 = [] #大根堆，存的相反数
for i in range(p,q+1):
  maxt = max(maxt,f[i])
  mint = min(mint,f[i])
  heapq.heappush(h2,f[i])

#向左拓展
for i in range(p-1,0,-1):
  maxt = max(f[i],maxt)
  heapq.heappush(h2,f[i])
  heapq.heappop(h2)
  mint = h2[0]
  res = max(res,maxt-mint)

print(res)