完全搞懂二分

看完了灵神 20 分钟的二分讲解，把以前看了好多遍都没看懂的二分彻底理解了，开心~

主题：红蓝染色法理解二分，力扣152,163

二分

红蓝染色法理解二分

我们以寻找到 >= x 的第一个下标来举例：

你的条件可以灵活定义

用红色表示不满足条件的，蓝色表示满足条件的，白色表示不确定

核心：

• 你要维护的区间内的都是没有染色的，区间的定义是未染色的范围，而不是答案的范围！！！
• l 和 r 的初始值怎么定义？看你初始的不知道如何染色的区间范围（白色）是多少，以及你二分是使用闭区间 or 开区间 or 左闭右开 哪种策略编写的，据此定下来你的 l 和 r值
• 循环条件如何终止？当你的区间不为空的时候循环
• 中间判断了之后 l，r 与 m 的关系应该怎么变化：看你想要寻找什么
• 最后答案应该怎么return：在找第一个 >= x 的情况下你要return的应该是蓝色（true）的第一个

mid 表示正在询问的数

闭区间写法下我们如何取得答案？

有一个循环不变量保持着：

• L-1始终是红色
• R+1始终是蓝色
• 那么答案其实就是 蓝色的第一个，也就是L或者R+1

多种写法

三种写法：推荐开区间，中间l,r,m之间的判断关系简单

# 找 >= target 的第一个
def lower_bound(nums,target):
    l = -1
    r = len(nums)
    #开区间写法
    while l+1 < r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m   #(m,r)
        else:
            r = m #(l,m)
    return r

def lower_bound2(nums,target):
    #闭区间写法
    l = 0
    r = len(nums)-1
    while l<=r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m+1   
        else:
            r = m-1 
    return l

def lower_bound3(nums,target):
    l = 0
    r = len(nums)
    #左闭右开区间写法 
    while l < r: #区间不为空
        m = (l+r) // 2
        if nums[m] < target: #false
            l =  m+1   
        else:
            r = m 
    return r
PYTHON

那么一共演变了四种题型：

>= x 	这种是我们熟知的
> x 	这种可以转化为 >= x+1
< x 	这种可以转为 >=x 的下标 -1
<= x	这种可以转为 >x 的下标 -1 即 >= x+1
LLVM

如果说target比所有的数都大的话：会返回数组最大下标的next

target比所有的数都小的话：会返回 0

target在最大最小范围内，但是没有target，会返回 >= target 的第一个

python 写二分最好还是直接调用库，这样比较快，大概快一半

from bisect import *
bisect_left(nums,target) #返回 >= target的第一个，行为与我自己写的完全一致
PYTHON

162

https://leetcode.cn/problems/find-peak-element/

#红色代表峰顶左边
#蓝色代表峰顶以及峰顶右边
#区间表示不知道染什么色的东西
#只需要比较mid和mid+1就行，找到第一个下坡？
#如果你往下坡方向走，也许可能遇到新的山峰，但是也许是一个一直下降的坡，最后到边界。
#但是如果你往上坡方向走，就算最后一直上的边界，由于最边界是负无穷，所以就一定能找到山峰
#总的一句话，往递增的方向上，二分，一定能找到，往递减的方向只是可能找到，也许没有
def lower_bound(nums):
    l = -1 #[0,n-2]
    r = len(nums) - 1
    while l+1<r:
        mid = (l+r) // 2
        if nums[mid] < nums[mid+1]:
            l = mid #染红色
        else:
            r = mid #染蓝色
    return r
class Solution:
    def findPeakElement(self, nums: List[int]) -> int:
        return lower_bound(nums)
PYTHON

153

原题链接： 153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

分析

这题一共就两种情况，因为是对一个有序数组的旋转，看下面画的图

第一种情况很好解决，简单的二分，第二种情况需要分析一下

image-20240509180447566

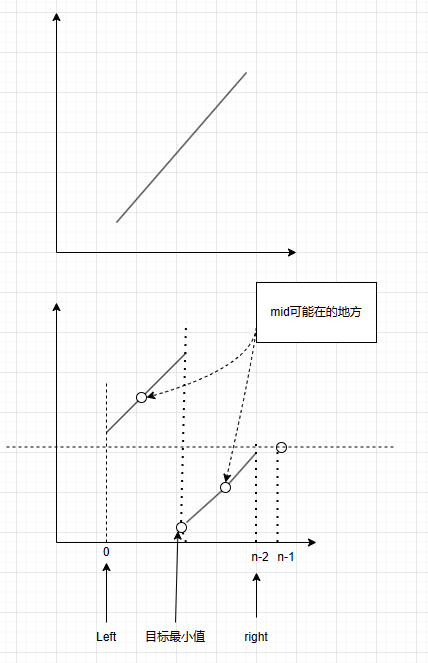
我们要找的相当于是谷底，也就是左右都比他大的

红蓝染色法二分：

• 红色表示最小数的左边
• 蓝色表示最小数或者最小数的右边

我们可以首先确定最后一个数一定是蓝色，所以开始的区间可以设为 [0,n-2]，这个区间是我们不知道要怎么染色的，接下来开始二分缩小这个区间

使用开区间来写的话，最初 l = -1，r = n-1

那么我们怎么确定要染什么颜色？

• 通过已知条件来看，我们仿照上一题，让mid和mid+1来比较可以吗？显然是不行的，因为除了最小值旁边的元素其他位置都满足 num[mid] < num[mid+1] ，无法根据这个来染色
• 可以根据 num[mid] 和 num[-1] (最后一个元素) 来比较
  • 如果 num[mid] < num[-1]：由图可知，需要让 r = mid
  • 如果 num[mid] > num[-1]：由图可知：需要让 l = mid

最后返回值应该是什么呢，下标返回 r 即可

code

# 这题不就是寻找谷值吗
# 红色表示谷左边
# 蓝色表示谷以及谷的右边
def binsearch(nums):
    l = -1 # [0,n-2]
    r = len(nums) - 1
    while l+1 < r:
        mid = (l+r) // 2
        if nums[mid] < nums[-1]:
            r = mid 
        else:
            l = mid
    return nums[r]
class Solution:
    def findMin(self, nums: List[int]) -> int:
        return binsearch(nums)
PYTHON

思考：

边界条件，最小的在最右怎么办?

• 这种情况由于一开始其实我们就给最右染色了，那么 r 一直是不会移动的，合理