从BST到高维数据search

quadTree，kdTree

Lecture 19: Multi-Dimensional Data

Range-Finding and Nearest (1D Data)

BST中可添加的operation：

• select(int i): Returns the ith smallest item in the set.
• rank(T x): Returns the “rank” of x in the set (opposite of select).
• subSet(T from, T to): Returns all items between from and to.
• nearest(T x): Returns the value closest to x.
  • 实现：Just search for N and record closest item seen

直到现在，我们总是在一维数据中比较，但是不是所有的item都能只在一个维度中完成比较的

Multi-dimensional Data

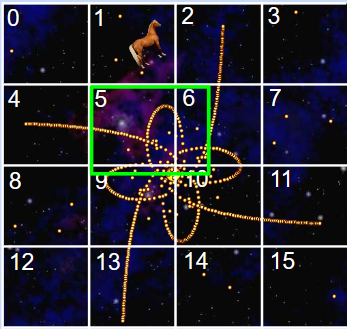
我们想在二维空间中实现

• 2D Range Searching: How many objects are in the highlighted rectangle(矩形)? 注意这个操作其实就是上面一维数据中的subset的推广
• Nearest

Ideally, we’d like to store our data in a format (like a BST) that allows more efficient approaches than just iterating over all objects.

BST of 2D

我们需要做出选择，是以x坐标比较(X-Based Tree)，还是以y坐标(Y-Based Tree)比较来建立我们的BST，无论哪一种，我们都会丢失掉一些信息，这会让我们的search变慢

QuadTrees

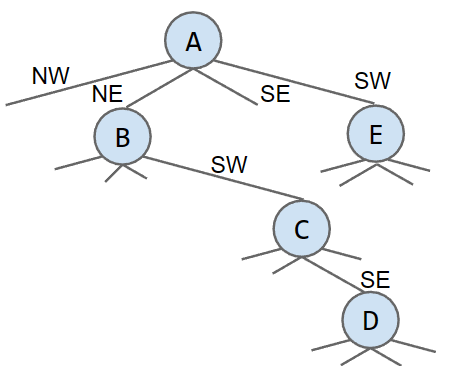
类似x，y坐标系，我们将2D空间分出四部分，NW(西北)，NE(东北)，SW(西南)，SE(东南)

Every Node has four children:

• Top left, a.k.a. northwest.
• Top right, a.k.a. northeast.
• Bottom left, a.k.a. southwest.
• Bottom right, a.k.a. southeast.

注意，在插入生成QuadTrees时，我们也需要沿着root出发，再依次顺着树枝往下走，直到找到合适的地方插入

QuadTrees Insertion Demo

Range Search Demo

以上是2D情况，对于3D，我们可以用8叉树来表示空间并进行高效地search，以此类推，来表示更高维度(大于3 dimensions的数据真的存在吗，有什么用？You may want to organize data on a large number of dimensions.Example: Want to find songs with the following features:Length between 3 minutes and 6 minutes.Between 1000 and 20,000 listens.Between 120 to 150 BPM.Were recorded after 2004.)

我们可以简单地增加子结点的个数，但这会显得臃肿，因此我们引出一种简洁但是对任何维度都适用的——k-d Tree

k-d Tree

有点类似于我们最早提出BST的X-Based Tree and Y-Based Tree，但是有所改进，对于2D，我们对于每一层比较的标准是按照顺序x-y-x-y…，3D(x-y-z-x-y-z…)

k-d tree example for 2-d:

• Basic idea, root node partitions entire space into left and right (by x).
• All depth 1 nodes partition subspace into up and down (by y).
• All depth 2 nodes partition subspace into left and right (by x).

K-d tree insertion demo.

k-d Tree对待比较中的平局，可以看做大于 or 小于，选定了就不能再改变了。

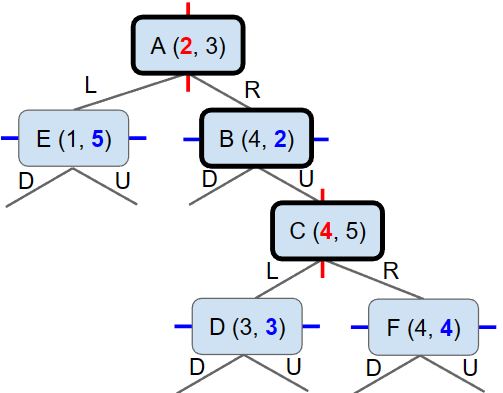
k-d nearest (始终是沿着建立好的k-d Tree来搜索)

• You always explore the good side [the old version performed an unnecessary check!
• You only explore the bad side if there’s a chance that it could contain something better.

k-d nearest，先看好的一方，在判断坏的一方是否值得一看

nearest(Node n, Point goal, Node best):
	If n is null, return best
	If n.distance(goal) < best.distance(goal), best = n
	If goal < n (according to n’s comparator):
		goodSide = n.”left”Child
		badSide = n.”right”Child
	else:
		goodSide = n.”right”Child
		badSide = n.”left”Child
	best = nearest(goodSide, goal, best)
	If bad side could still have something useful
		best = nearest(badSide, goal, best)
	return best

Uniform partitioning

把空间均分为几部分(类似hashtable中的bucket)，然后将数据存储在bucket中