排序算法专题

CS61B排序：选择排序，堆排序，归并排序，插入排序，希尔排序，快排

Sort

inversion(逆序对)

• An inversion is a pair of elements that are out of order with respect to <.

一种看待sort的方法：

• Given a sequence of elements with Z inversions.
• Perform a sequence of operations that reduces inversions to 0.

Sort中，我们关注两种复杂度

• time complexity
• space complexity (extra memory usage)

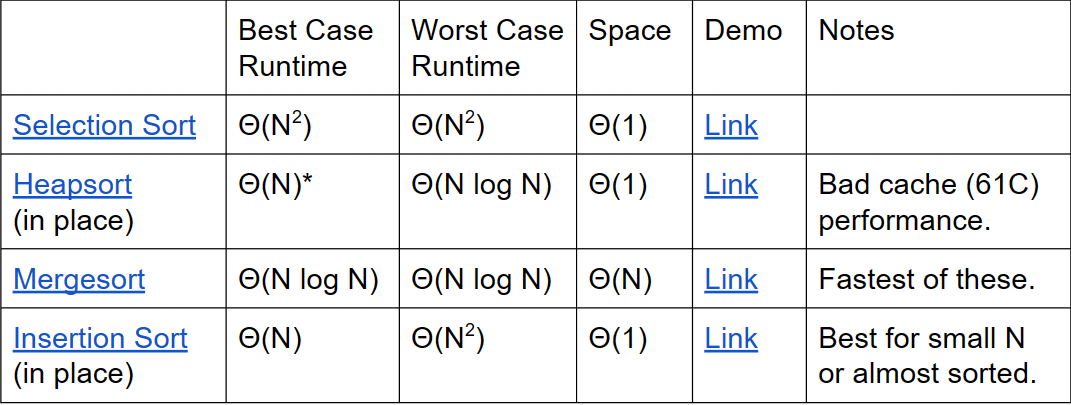
Selection Sort

θ(N^2^)

• Find smallest item.
• Swap this item to the front and ‘fix’ it.
• Repeat for unfixed items until all items are fixed.

Heap Sort

基于Selection Sort，但是加速了找smallest item这个过程

必须用max-heap，why？

• min-heap也可以work，但是我们如果想直接在该数组中建立堆(without extra output array)来节省space complexity，min-heap不能做到这点

naive(朴素版)heap sort

• Insert all items into a max heap, and discard input array. Create output array.
• Repeat N times:
  • Delete largest item from the max heap.
  • Put largest item at the end of the unused part of the output array.

runtime

• time complexity：θ(NlogN)
• space complexity：θ(N) 因为开辟了额外的输出数组，长度为N
  • 这比选择排序worse，但是我们下面的策略可以改进

In-place Heapsort

no extra array，直接在原数组中建立堆(heapify)，之后和朴素版的heapsort就一致了

为什么可以这样？因为按照层序从后往前的过程中，我们sink之后就保证以该位置为root的一个子堆满足heap的性质，因此我们从小到大地建立了完整有效地堆

• Bottom-up heapify input array.
  • To bottom-up heapify, just sink nodes in reverse level order.
  • After sink(k), guaranteed that tree rooted at position k is a heap.
• Repeat N times:
  • Delete largest item from the max heap, swapping root with last item in the heap.

in-place heap sort Demo

runtime

• time complexity：θ(NlogN)
• space complexity：θ(1)

Merge Sort

chapt 8里面讲过，依次挨个地合并两个有序的数组

看这个Demo就理解了 Merge Sort Demo

• Split items into 2 roughly even pieces.
• Mergesort each half (steps not shown, this is a recursive algorithm!)
• Merge the two sorted halves to form the final result.
  • Compare input[i] < input[j] (if necessary).
  • Copy smaller item and increment p and i or j.

insertion sort

naive

• Starting with an empty output sequence.
• Add each item from input, inserting into output at right point.

in-place

• 在该数组内用swap，而不是再开一个数组
• Repeat for i = 0 to N - 1:
  • Designate item i as the traveling item.
  • Swap item backwards until traveller is in the right place among all previously examined items.

note：

对于差不多有序的序列来说很快

runtime与inversion(逆序对)的个数成正比

一些经验表示，对于<15个元素的序列，insertion sort是所有排序中最快(粗略的解释：Divide and conquer algorithms like heapsort / mergesort spend too much time dividing, but insertion sort goes straight to the conquest.)

Shell Sort

利用insertion对元素少的序列很快这一特点

• 将序列中，每间隔d的index分为一组，对该组进行insertion sort
• 不断d--，直到d=1，整个序列恰恰都在一组，完成排序

Quick Sort

一个好的quick sort：需要有

• pick good pivot
• good partition strategy

Quicksorting N items: (Demo)

The Core Idea of Tony’s Sort: Partitioning

To partition an array a[] on element x=a[i] is to rearrange a[] so that: (partition作用的那个i，就叫做pivot)

• x moves to position j (may be the same as i)
• All entries to the left of x are <= x.
• All entries to the right of x are >= x.

实现：

• 可以用BST，把pivot当做root，比他小的都在left，比他大的都在right
• simple but not fastest: 3 scan
  • Create another array. Scan and copy all the red items to the first R spaces. Then scan for and copy the white item. Then scan and copy the blue items to the last B spaces.

observations:

• 当我们partition(k=a[i])之后，k就在它的最终位置上不动了了(左边的都比他小，右边的都比他大)
• Can sort two halves separately, e.g. through recursive use of partitioning.左右两边完全独立了

步骤：

• Pick the pivot to be partitioned: e.g.Partition on leftmost item.
• Quicksort left half.
• Quicksort right half.

runtime

• 值得一提的是，quick sort的速度与选取的pivot最终落在的位置有很大关系

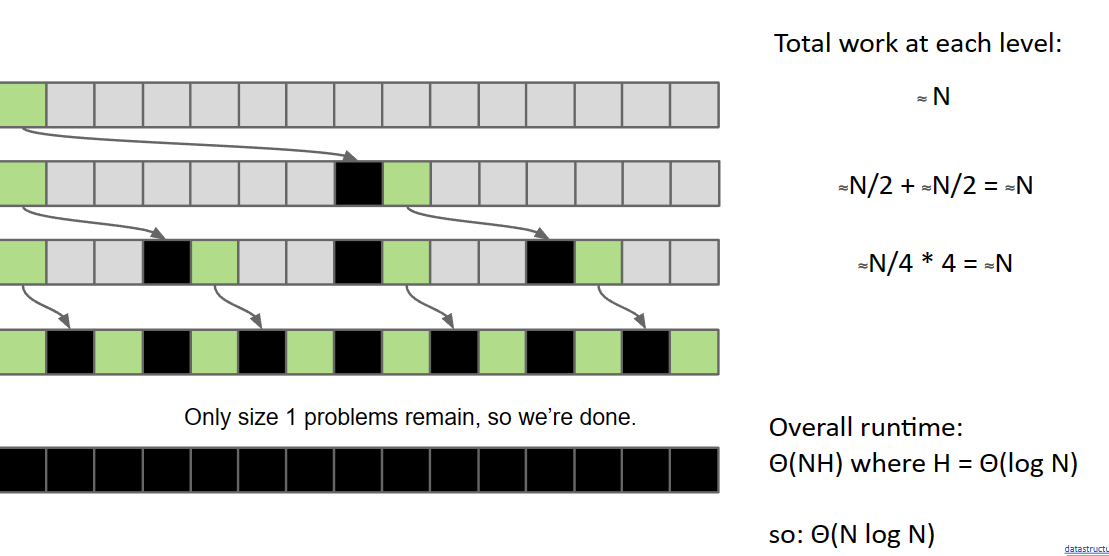
Best Case: Pivot Always Lands in the Middle

递归深度logN

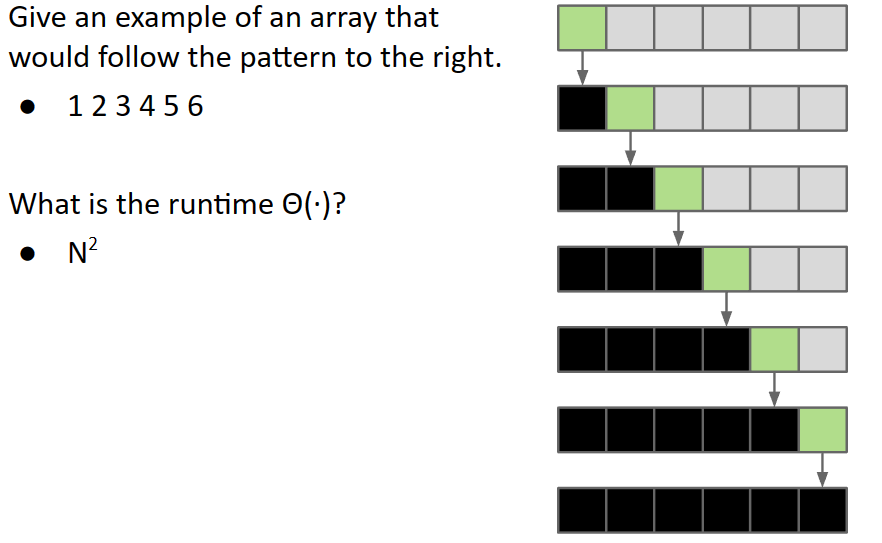
Worst Case: Pivot Always Lands at Beginning of Array

递归深度N

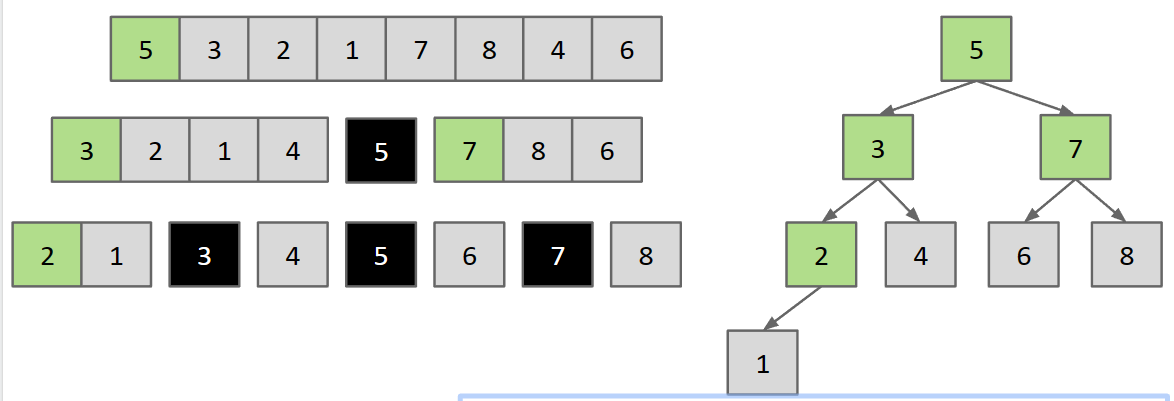
一个有趣的观察：

• Quick Sort的过程其实就是BST建立的过程，我们可以看到每次选取的pivot都是子树的一个根，向下建立BST，so crazy！
• 回想Random insertion into a BST takes O(N log N) time.

问题来了，N^2^与NlogN的差别可谓巨大，所以我们该怎么避免worst case的出现？

Avoiding the Quicksort Worst Case

小心两种特殊的序列，他们可能会使你的策略陷入N^2^

• Bad ordering: Array already in sorted order.
• Bad elements: Array with all duplicates.

we mainly focus on

• How you select your pivot.
• How you partition around that pivot.

Philosophy 1: Randomness

随机性是一个好的Quick Sort所必需的，对于一些确定的or伪随机的，总会存在潜在的危险. See McIlroy’s “A Killer Adversary for Quicksort”

• Strategy #1: Pick pivots randomly.
• Strategy #2: Shuffle(搅乱) before you sort.

Philosophy 2b: Smarter Pivot Selection

Use the median (or an approximation) as our pivot.也就是选取的pivot正好落在中间

利用partition来寻找中值pivot

• 一直partition，让partition(k)之后k的位置往中间靠，直到k落在length/2的位置

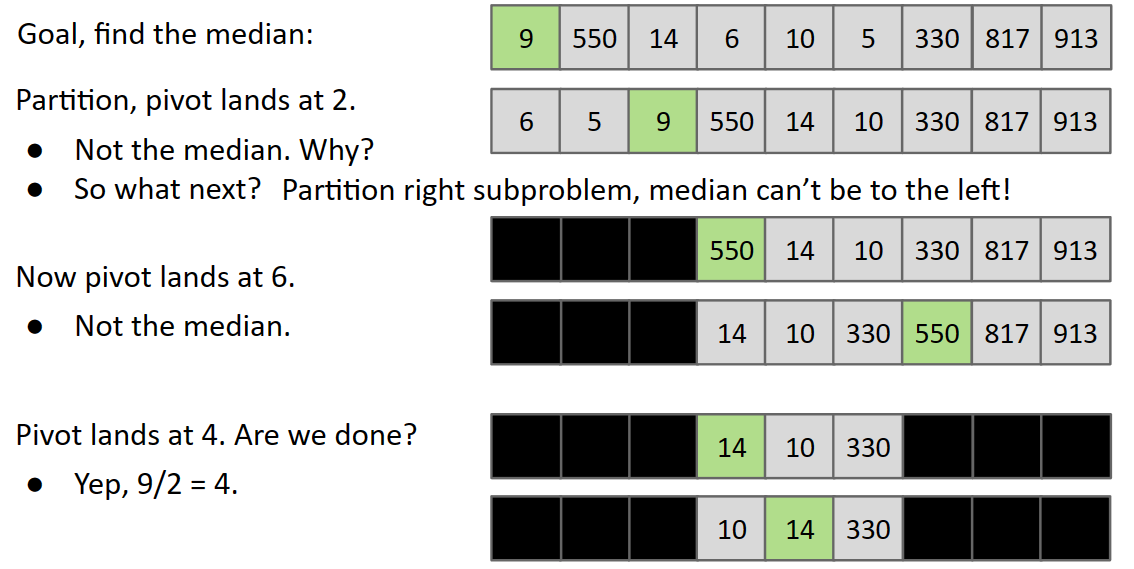
worst case：θ(N^2^) i.e.[1 2 3 4 5 6 7 8 9 10 … N]

average case：θ(N)

Hoare Partitioning(双指针法)

Demo

Create L and G pointers at left and right ends.

• L pointer is a friend to small items,and hates large or equal items.(注意对于equal的我们不管，不然对于全重复元素的序列我们会陷入worst case)

• G pointer is a friend to large items,and hates small or equal items.

• Walk pointers towards each other,stopping on a hated item.

  • When both pointers have stopped,swap and move pointers by one.

  • When pointers cross,you are done walking.

• Swap pivot with G.

Sorting Properties

stability

• Equivalent items don’t ‘cross over’ when being stably sorted.