BST与平衡树

CS61B的BST，B树，23树，红黑树，LLRB 原理

Chapt10 ADTs, Sets, Maps, BSTs

加快链表的查找也可以使用跳表来优化 θ(logN)

BST(Binary Search Tree)

一篇好文It’s Triangles All the Way Down (Part 1) | by Amy Liu | Medium

二分查找树

提出BST的原因

• 对于LinkedList来说，我们search时最坏情况需要遍历整个list，尽管list是有序的，对于ordered array来说，我们可以通过二分查找来加快查找速度
• 受array的启发，我们可以在LinkedList的middle node设置一个引用，然后将middle node左边的List的指向翻转，这样我们就可以从middle位置根据大小向两边查找了
• 我们可以做得更好，在左右部分，递归地，我们继续添加他们各自middle node的使用，直到每个部分只剩1个，这就会形成BST

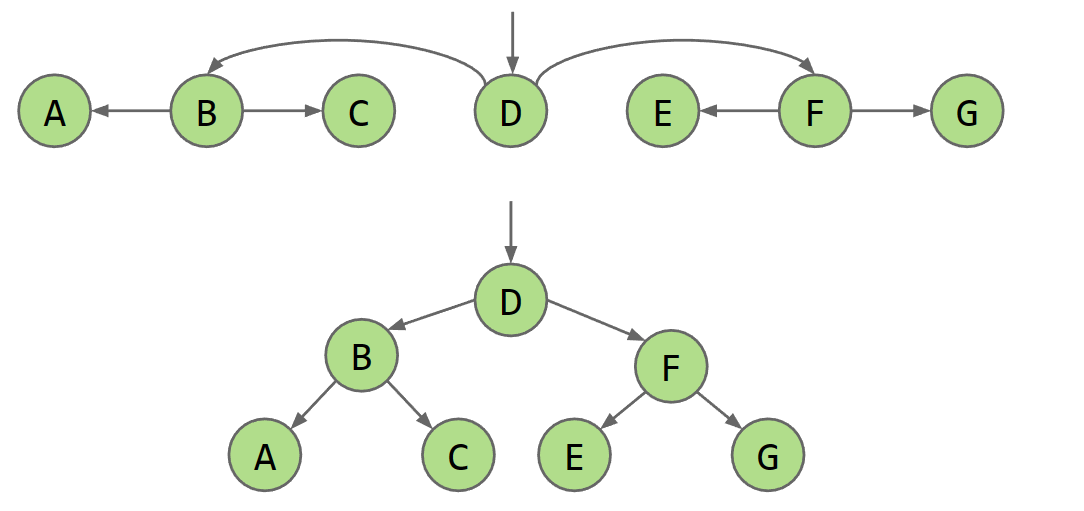
• Binary Search Trees:
  • Every key in the left subtree is less than X’s key.
  • Every key in the right subtree is greater than X’s key.

private class BST<Key> {
    private Key key;
    private BST left;
    private BST right;

    public BST(Key key, BST left, BST Right) {
        this.key = key;
        this.left = left;
        this.right = right;
    }

    public BST(Key key) {
        this.key = key;
    }
}

BST operations

• static BST find(BST T, Key key)

  • T是BST的root，return 与key匹配的node

  • ```java
    static BST find(BST T, Key sk){

    if(T==null){
        return null;
    }
    if(sk.equals(T.key)){
        return T;
    }else if(sk<T.key){
        find(T.left,sk);
    }else if(sk>T.key){
        find(T.right,sk);
    }
    

    }

    * `static BST insert(BST T, Key ik)`
    
      * 我们总是在叶子结点进行insert！
    
      * return the full BST with the new node inserted in the correct position.
    
      * BST 不能有重复的
    
      * If found, do nothing.
    
      * If not found:
    
        * Create new node.
        * Set appropriate link
    
      * ```java
        static BST insert(BST T, Key ik){
            if(T==null){
                return new BST(ik);
            }
            if(ik<T.key){
                T.left=insert(T.left,ik);
            }else if(ik>T.key){
                T.right=insert(T.right,ik);
            }
            return T;
        }

• static BST delete(BST T,key dk)

  • Hibbard deletion

  • has no children

    • 删除的肯定是叶子结点，只需要改变该叶子结点的父亲，

  • has 1 child

    • 把该结点父亲结点的pointer指向该结点的子结点 we can just reassign the parent’s child pointer to the node’s child and the node will eventually be garbage collected

  • has 2 children

    • 目标是找到一个满足左边的都比他小，右边都比他大的node来代替需要删除的node

    • 删除有两个子结点的：对该子树，选择该子树中，左边最右(predecessor)，或者右边最左(sucessor)的来代替root

      

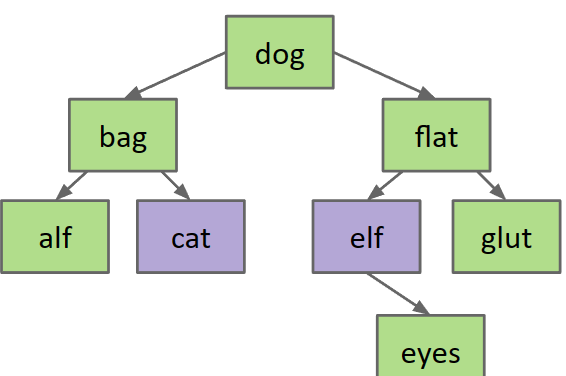
θ(logN)：This was because we could eliminate half of the elements at every step of our search

Chapt11：Balanced Trees

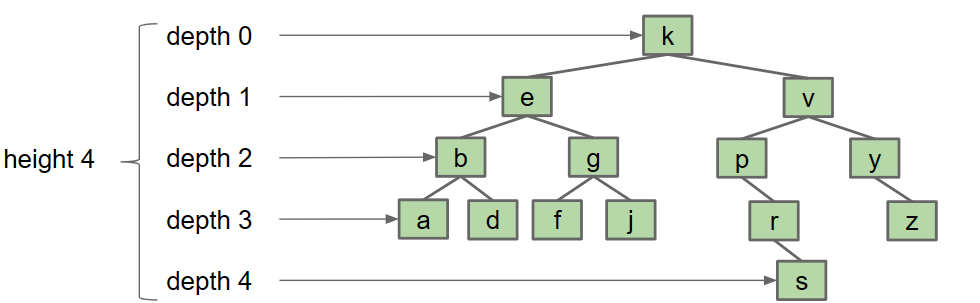
• The depth of a node：距离根结点有多远
• The “height” of a tree is the depth of its deepest leaf, e.g. height(T) = 4. worst case
• The “average depth” of a tree is the average depth of a tree’s nodes. average case
  • (0x1 + 1x2 + 2x4 + 3x6 + 4x1)/(1+2+4+6+1) = 2.35

BSTs have:

• Worst case Θ(N) height.
• Best case Θ(log N) height.

对于BST来说，不同的插入顺序会形成不同height的tree，也会造成不同的查找速度

Randomlized Trees

现实中插入往往是随机的，已经证明，随机插入的tree

• average depth：~ 2 ln N = Θ(log N)
• height：~ 4.311 ln N= Θ(log N)
• note：~ 和 Θ是一样的，但没有丢掉常数

因此，随机插入时BST的表现不错，但是现实中我们不能做到处处随机，因此我们引出B-Trees来解决这个问题(在任意插入顺序下都有很好的height)

B tree

BST的问题是：我们一直在叶结点之后插入，这会导致height增加；那么，我们是否可以一直不往叶结点插入，来保证tree balance

可以处理任何输入顺序，让树饱满，平衡

Avoiding Imbalance through Overstuffing

• Never add new leaves at the bottom.
• just add to a current leaf node.

这也会造成一个问题，我们的叶子结点承载了太多(Leaf nodes can get too juicy.)，在叶子结点内的search是Θ(N)，退化了

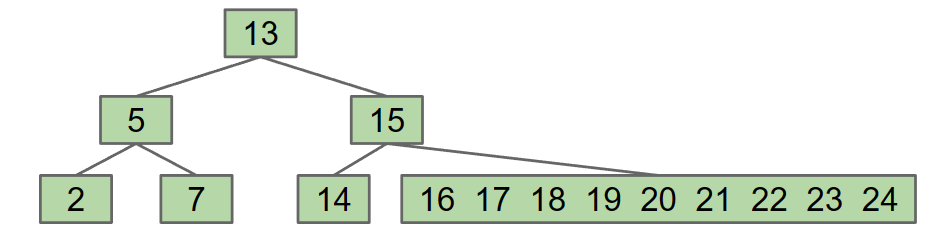
solution

• Set a limit L on the number of items, say L=3.
• If any node has more than L items, give an item to parent.
  • Which one? Let’s say (arbitrarily) the left-middle. 超载时有4个，选取中间靠左那个向上移
  • 移了之后re-arrange the children accordingly.

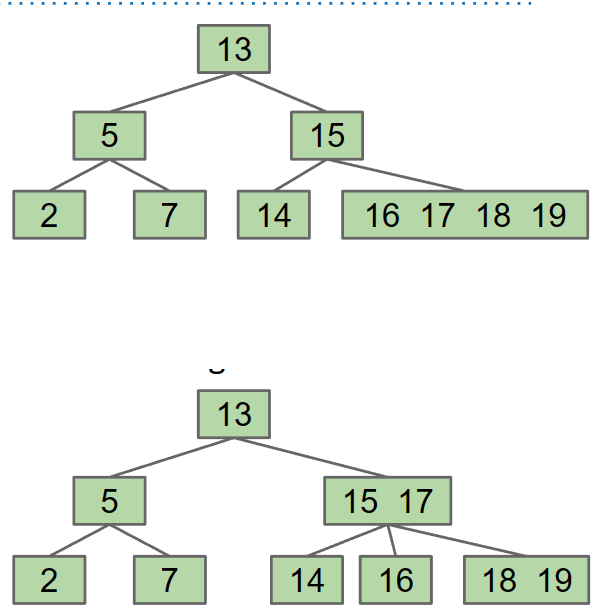
这些树被称作B-Tree or 2-3-4 tree or 2-3 tree，2-3-4的意思是每个结点的子结点可能有2,3,4之一

The process of adding a node to a 2-3-4 tree is:

1. We still always inserting into a leaf node, so take the node you want to insert and traverse down the tree with it, going left and right according to whether or not the node to be inserted is greater than or smaller than the items in each node.
2. After adding the node to the leaf node, if the new node has 4 nodes, then pop up the middle left node and re-arrange the children accordingly.
3. If this results in the parent node having 4 nodes, then pop up the middle left node again, rearranging the children accordingly.
4. Repeat this process until the parent node can accommodate or you get to the root.

Observation: Splitting-trees have perfect balance.

• 如果分裂root，那么每个结点正好被压低一级，height+1
• 如果分裂叶子结点或者内部的结点，height不变
• 对于B树来说，不管是怎样的插入顺序，B-Tree都是稠密的，尽管可能在height上有细微的差别

B-Tree Invariants

由于B-Tree生成的独特方式，有以下不变的性质

• 所有的叶结点到root的距离都相等
• 所有的非叶结点node有k个，那么它的子结点一定有k+1个

这些不变量保证了B-Tree的稠密

B-Tree runtime

L: Max number of items per node.
Height: Between ~logL+1(N) and ~log2(N)

最高是每个叶子结点只包含一个，最低是每个叶子结点包含L个

• contains O(logN)
• add O(logN)

2-3 Tree Deletion

In a 2-3 Tree, when we delete α from a node with 2 or more children, we:

• Swap the value of the successor with α. note:Successor will always be in a leaf node

• Then we delete the successor value.

  • **Multi-Key Leaves **

    • simply remove the item from the leaf

      

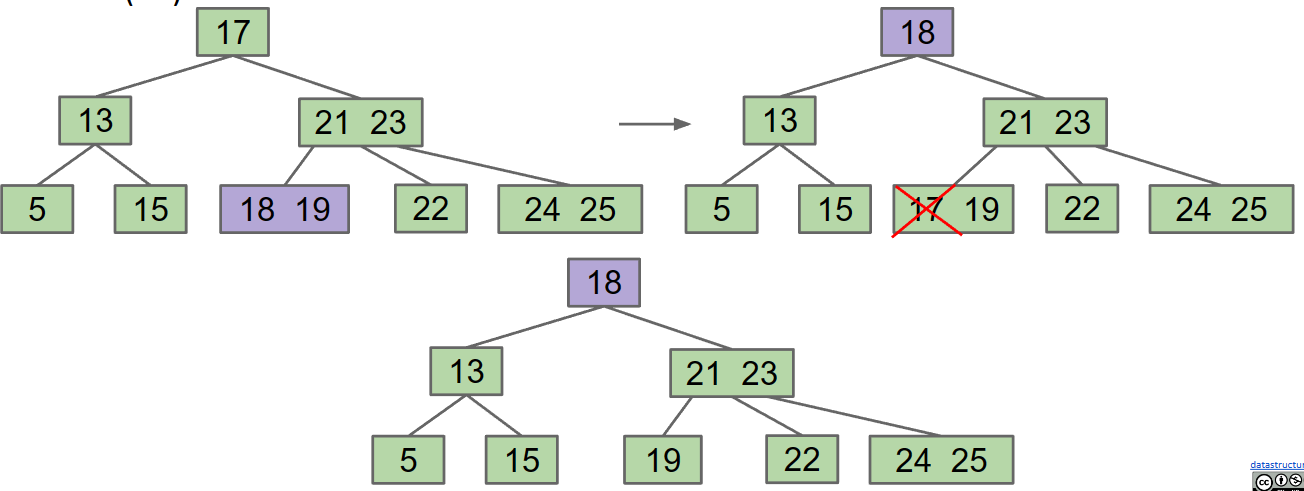
  • Single-Key Leaves

    • cannot simply remove the node entirely (Any node with k items must have k + 1 children! Instead, we’ll leave an empty node, which must be filled.)
    • so how to Filling in Empty Nodes (FIEN)?

Filling in Empty Nodes (FIEN)

1. 兄弟结点 Mutil-key Sibling

   • X steals parent’s item. Parent steals sibling’s item.

   • If X was not a leaf node, X steals one of sibling’s subtrees (to keep is a B-Tree).

   • x不是叶子结点

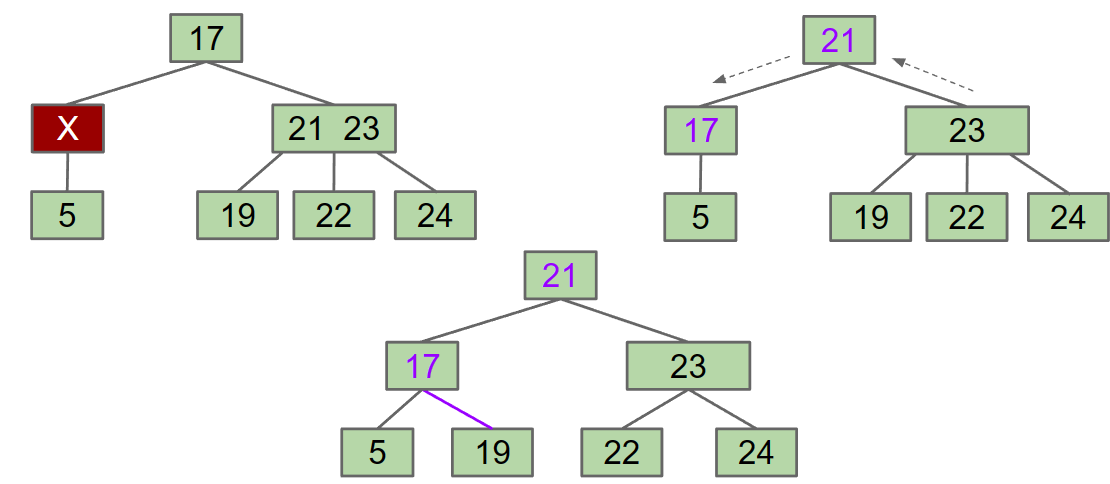
   • x是叶子结点

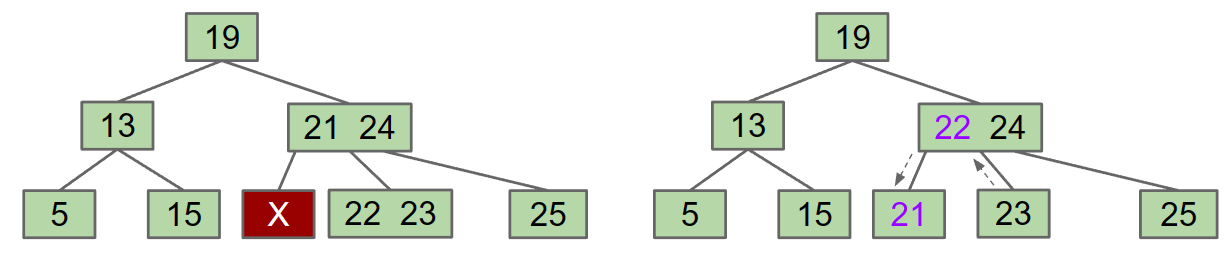
2. Multi-key parent ( siblings on the right all have one key)

   • X and right sibling steal parent’s keys. Middle sibling moves into the parent.
   • Subtrees are passed along so that every node has the correct children.
   • 

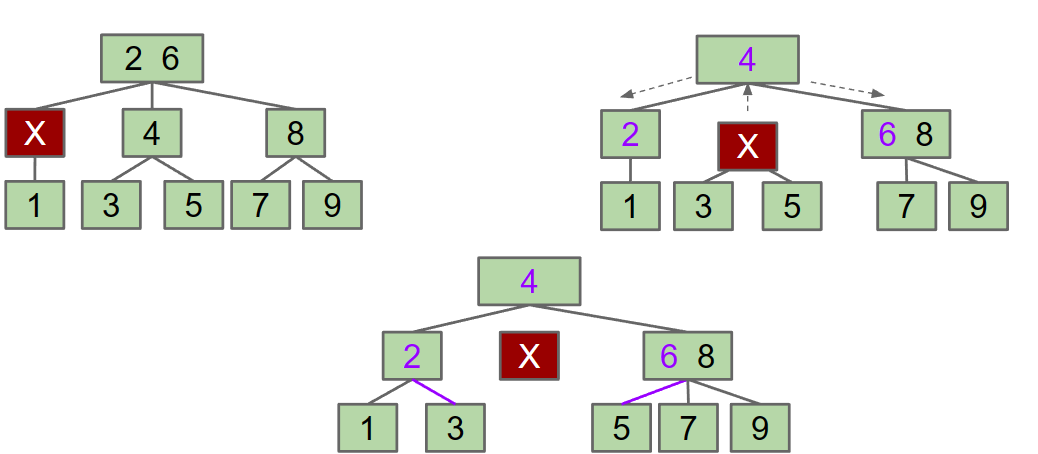
3. single-key parent and Sibling( The parent and all siblings have only one item.)

   • Combine 1 sibling and parent into a single node that replaces X. Send the blank X up one level.
   • If blank ends up as the new root, just delete the blank and we are done.
   • 

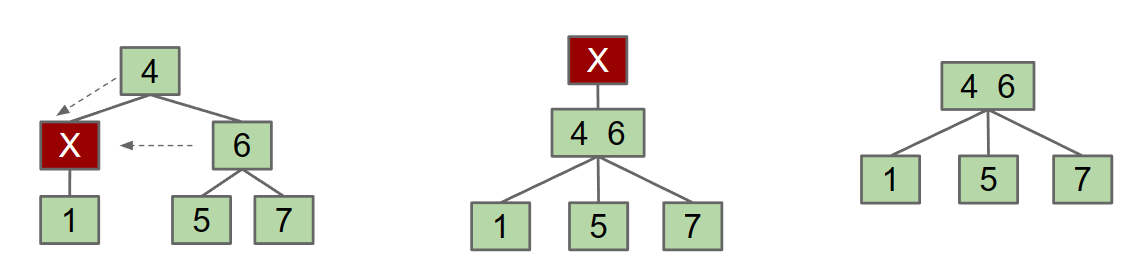
BST Rotating Tree

B-Tree实现起来很困难，尽管他快，让我们找另外一种同样快且实现简单的方法

由于插入顺序的不同，会形成多种B-Tree，其数目是可以计算的catalan(卡特兰数) Catalan number - Wikipedia

rotate可以在O(N)的时间内将树旋转为稠密的 (can move from any configuration to any other in 2n - 6 rotations )

The formal definition of rotation is:

rotateLeft(G): Let x be the right child of G. Make G the new left child of x.

• 另一种理解方式：将right的x与G合并，然后向下发送合并之后的left(也就是G)，然后调整树的结构使其符合BST

rotateRight(G): Let x be the left child of G. Make G the new right child of x.

• 把G和left的x合并，然后向下发送合并之后的right(也就是G)，然后调整树使其符合BST

不能rotate空的，无意义

private Node rotateRight(Node h) {
    // assert (h != null) && isRed(h.left);
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    return x;
}

// make a right-leaning link lean to the left
private Node rotateLeft(Node h) {
    // assert (h != null) && isRed(h.right);
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    return x;
}

在建造的时候保持稠密

Red-Black Tree

a specific tree data structure that remains balanced through using rotations.

一般的BST需要O(N)的时间来rotate来达到balance，这是在建造好之后采取的措施，亡羊补牢；下面介绍一种在建造的时候利用rotate来保持balance和bushy的结构

Our goal: Build a BST that is structurally identical to a 2-3 tree.Since 2-3 trees are balanced, so will our special BSTs.

一个很好的exercise LLRB Insertion Demo - Google 幻灯片

Representing a 2-3 Tree as a BST

A 2-3 tree的2-nodes(可以有两个子结点的结点)和BST的完全一致

对于3-nodes来说：两种可能的方法

1. “glue” node that doesn’t hold any information and only serves to show that its 2 children are actually a part of one node.

   
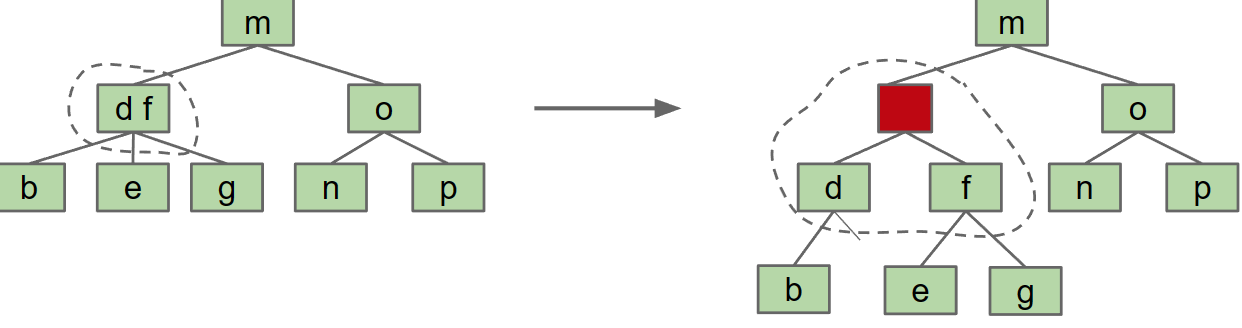
   • 缺点是不优雅，code will be ugly，而且d的right实际上浪费了

2. Create “glue” links with the smaller item off to the left (这种更好)

   • make the left element a child of the right one.

   • We show that a link is a glue link by making it red.

     

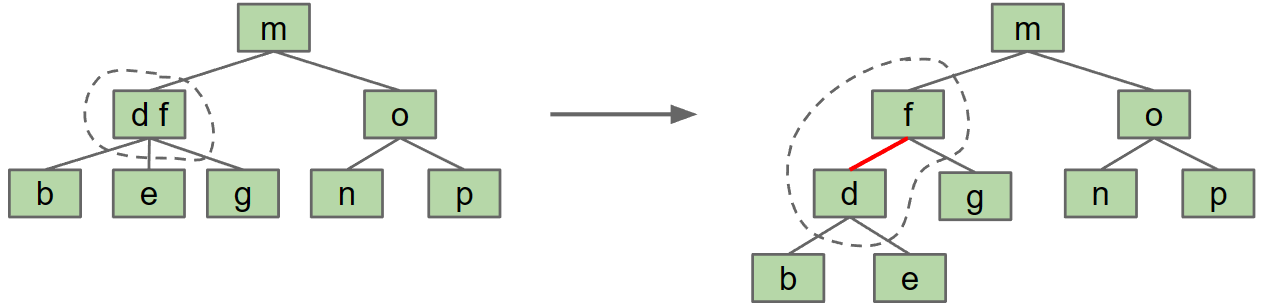
LLRB

A BST with left glue links that represents a 2-3 tree is often called a “Left Leaning Red Black Binary Search Tree” or LLRB.

• LLRBs are normal BSTs!
• There is a 1-1 correspondence between an LLRB and an equivalent 2-3 tree.
• The red is just a convenient fiction. Red links don’t “do” anything special.

LLRB’s的特征

Here are the properties of LLRB’s:

• 与 2-3 trees 1-1对应.
• No node has 2 red links.
• There are no red right-links.
• Every path from root to leaf has same number of black links (because 2-3 trees have same number of links to every leaf).
• Height is no more than ~2x height of corresponding 2-3 tree.

What is the maximum height of the corresponding LLRB? (看黑线和红线之和)

• Total height is H (black) + H + 1 (red) = 2H + 1.

LLRB Construction

• Insert as usual into a BST.
• Use zero or more rotations to maintain the 1-1 mapping.

Inserting into LLRB

为了保持LLRB与2-3树的1-1对应，我们需要在LLRB中处理2-3树插入的各种情况

1. Task 1: insertion color: 在2-3 tree中，我们总是向叶子结点add，因此link的颜色总是应该为红色

2. Task 2: insertion on the right: 回想一下，我们使用的是left-leaning的红色黑色树，这意味着我们永远不可能有一个right的红色链接。如果我们插入在右边，我们将需要使用旋转，以保持 LLRB 不变量。

   但是，如果我们将要在右边加入一个红色链接，而且其左边也是一个红色链接，我们暂时允许这种情况存在，后面解决这种illegal的情况

   

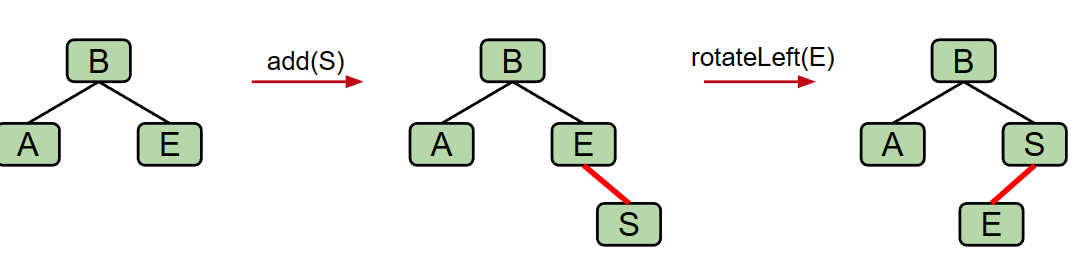
3. **Task 3: double insertion on the left:**（two consecutive left links）

   If there are 2 left red links, then we have a 4-node which is illegal. First, we will rotate to create the same tree seen in task 2 above.

   

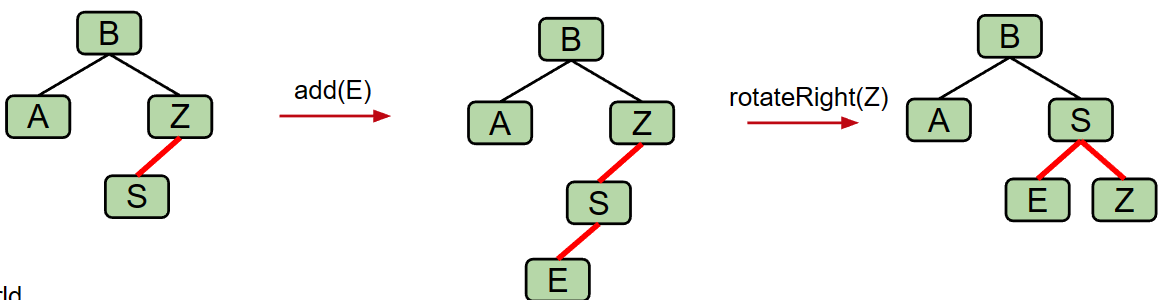
4. Splitting Temporary 4-Nodes：Then, in both situations, we will flip the colors of all edges touching S. This is equivalent to pushing up the middle node in a 2-3 tree.

   

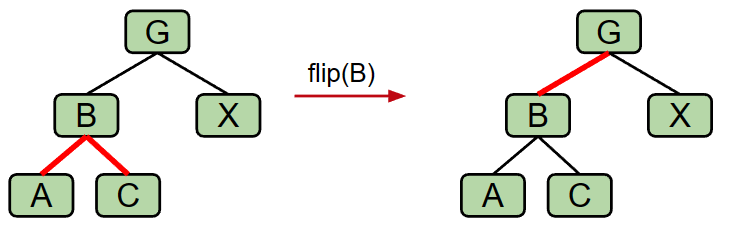
Here is a summary of all the operations:

• When inserting: Use a red link.
• If there is aright leaning “3-node”, we have a Left Leaning Violation
  • Rotate left the appropriate node to fix.
• If there are two consecutive left links, we have an incorrect 4 Node Violation!
  • Rotate right the appropriate node to fix.
• If there are any nodes with two red children, we have a temporary 4 Node.
  • Color flip the node to emulate the split operation.

• 注意这些情况可能会串联出现

Runtime :都是log(N)

Amazingly, turning a BST into an LLRB requires only 3 clever lines of code.Does not include helper methods (which do not require cleverness).

private Node put(Node h, Key key, Value val) {
    if (h == null) { return new Node(key, val, RED); }

    int cmp = key.compareTo(h.key);
    if (cmp < 0)      { h.left  = put(h.left,  key, val); }
    else if (cmp > 0) { h.right = put(h.right, key, val); }
    else              { h.val   = val;                    }
//只有下面这三行是额外添加的
    if (isRed(h.right) && !isRed(h.left))      { h = rotateLeft(h);  }
    if (isRed(h.left)  &&  isRed(h.left.left)) { h = rotateRight(h); }
    if (isRed(h.left)  &&  isRed(h.right))     { flipColors(h);      } 

    return h;
}

Summary

• Binary search trees are simple, but they are subject to imbalance which leads to crappy runtime.
• 2-3 Trees (B Trees) are balanced, but painful to implement and relatively slow.
• LLRBs insertion is simple to implement (but deletion is hard).
  • Works by maintaining mathematical bijection with a 2-3 trees.
• Java’s TreeMap is a red-black tree (but not left leaning).
• LLRBs maintain correspondence with 2-3 tree, Standard Red-Black trees maintain correspondence with 2-3-4 trees.
• Allows glue links on either side (see Red-Black Tree).
• More complex implementation, but significantly faster.