并查集

CS61B 的并查集，从原理到实现，WQU，路径压缩

chapt9 Disjoint Sets(并查集)

不同并查集的元素也不能相同，而且为正数

支持两个操作的数据结构

1. connect(x, y): connect x and y. Also known as union
2. isConnected(x, y): returns true if x and y are connected (i.e. part of the same set).

public interface DisjointSets {
    /** connects two items P and Q */
    void connect(int p, int q);

    /** checks to see if two items are connected */
    boolean isConnected(int p, int q); 
}

ListOfSets

最朴素的做法，List存set，List<Set<Integer>>

缺点：每次connect的时候需要遍历，O(N)，并且也不好写出

Implementation	Constructor	connect	isConnected
ListOfSets	Θ(N)1	O(N)	O(N)

Quick Find

• 数组的索引表示集合的元素
• The value at an index is the set number it belongs to.
• 只需要确保在一个集合中的元素有相同的id值就可以，这个值是什么并不重要

• connect：让两个集合的所有元素id改为相同
• isConnected(x, y)：we simply check if id[x] == id[y].

Implementation	Constructor	connect	isConnected
QuickFind	Θ(N)	Θ(N)	Θ(1)

Quick Union

不用id，我们在每个元素的索引存上他parent，如果没有parent，那么该元素为根，我们存上一个负数。这会让我们的集合看起来像个树形结构

we represent {0, 1, 2, 4}, {3, 5}, {6} as:

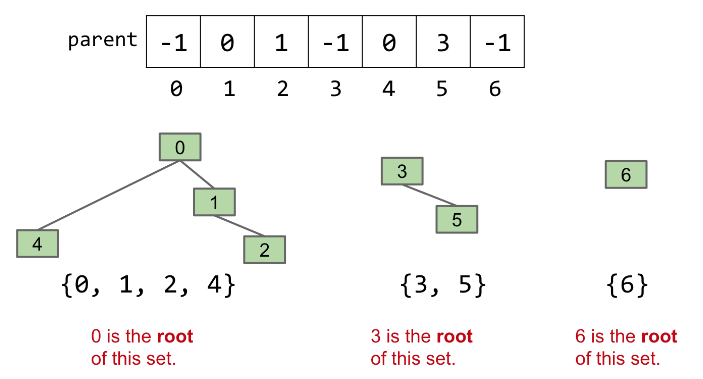
引入一个helper function： find(int item) which returns the root of the tree item is in. For example, for the sets above, find(4) == 0, find(1) == 0, find(5) == 3, etc. Each element has a unique root.

public int find(int x){
    while(parent[x]>0){
        x=parent[x];
    }
    return x;
}

• connect(x,y)：将x的parent改为y or 将y的parent改为x
• isConnected(x,y) ： check if find(x) == find(y).

Implementation	Constructor	connect（主要find操作耗时）	isConnected
QuickUnion	Θ(N)	O(N)	O(N)

Weighted Quick Union (WQU)

New rule: whenever we call connect, we always link the root of the smaller tree to the larger tree.

遵循这个规则，我们的tree高度不会超过logN，N是并查集元素的数量，因此the runtimes of connect and isConnected are bounded by O(log N).

既可以用数量，也可以用高度来衡量大小，两者的效率不会差太多，但是高度写起来很麻烦，因此我们常用集合数量来衡量

Implementation	Constructor	connect	isConnected
Weighted Quick Union	Θ(N)	O(log N)	O(log N)

WQU with path compression(路径压缩)

The clever insight is realizing that whenever we call find(x) we have to traverse the path from x to root. So, along the way we can connect all the items we visit to their root at no extra asymptotic cost.

Connecting all the items along the way to the root will help make our tree shorter with each call to find.

Implementation	isConnected	connect
Quick Find	Θ(N)	Θ(1)
Quick Union	O(N)	O(N)
Weighted Quick Union (WQU)	O(log N)	O(log N)
WQU with Path Compression	O(α(N))*	O(α(N))*